 Artist’s interpretation of “supercoupling” of light from an input and output waveguide, transmitted without reflection through an arbitrarily distorted, zero-index (ZI) obstacle. [Illustration by Ella Marushchenko and Alexander Tokarev]
Artist’s interpretation of “supercoupling” of light from an input and output waveguide, transmitted without reflection through an arbitrarily distorted, zero-index (ZI) obstacle. [Illustration by Ella Marushchenko and Alexander Tokarev]
Light and electromagnetic fields can propagate in vacuum at the maximal speed achievable—the speed of light. This characteristic, while invaluable for fast, long-range communications systems, also raises challenges for control and manipulation, making light virtually impossible to store.
Yet because light also interacts with matter, macroscopic media can be used to harness and manipulate light. And the possibilities of controlling light with matter are boosted still further through the use of metamaterials—carefully crafted media whose constituent elements have a structure and arrangement that enables distinct forms of interaction with and control of light, including bending, focusing, shaping, cloaking and even performing mathematical operations with light.
Not surprisingly, some unique features in wave interaction with metamaterials involve media with extreme material parameters, such as “zero-index” (ZI) media—media for which the refractive index n = (με)½ ≈ 0. These include, epsilon-near-zero (ENZ; ε ≈ 0), mu-near-zero (MNZ; μ ≈ 0) as well as epsilon-and-mu-near-zero (EMNZ; ε ≈ 0, μ ≈ 0) structures. Together, these media create new forms of wave dynamics defying our conventional intuitions.
The interplay between light and geometry in the ZI regime can enable the exploration of new physical mechanisms in classical and quantum electrodynamics.
Within the ZI regime, even a concept as basic as geometry may play a qualitatively different role in light-matter interactions, leading to measurable quantities, such as resonance frequency, that are invariant under geometrical transformations. That geometric invariance is exciting, as it could lead to development of deformable optical devices and flexible photonics. Moreover, the complex interplay between light and geometry in the ZI regime can enable the exploration of new physical mechanisms in both classical and quantum electrodynamics.
Here, we review a few of the more striking aspects of light propagation and trapping with ZI metamaterials.
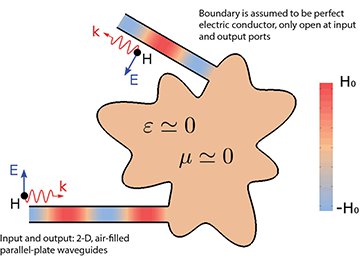 Supercoupling and deformable optics: In materials with permittivity and permeability near zero at a given operating frequency, an incoming wave can be transmitted without reflection through structures and obstacles of arbitrary cross-sectional shape, provided a continuous path can be drawn through the obstacle.
Supercoupling and deformable optics: In materials with permittivity and permeability near zero at a given operating frequency, an incoming wave can be transmitted without reflection through structures and obstacles of arbitrary cross-sectional shape, provided a continuous path can be drawn through the obstacle.
Supercoupling and deformable optics
According to one of our most basic intuitions, when a propagating electromagnetic wave encounters an obstacle, the wave scatters in various directions. Similarly, guided light, such as waves propagating within a microwave rectangular waveguide or optical fiber, is partly backscattered when it encounters an obstacle, such as a deformation of the guiding device or a sharp bend in the waveguide. In general, the deformation’s properties determine the amount of reflection, which typically increases as the geometry of the deformed section deviates more and more from that of an unperturbed channel.
Media with near-zero parameters, however, pose a challenge to this intuitive behavior. Indeed, EMNZ media (media with both zero permittivity and zero permeability at a given operating frequency) can, under certain circumstances, enable the full transmission of light through a distorted channel. Even more strikingly, this effect takes place independently of the geometry of the deformation.
In other words, a transverse electromagnetic (TEM) propagation channel filled with EMNZ media can be arbitrarily deformed without introducing any reflection. The only requirement is that the EMNZ region remains path-connected—that is, to ensure the transmission of light, it must be possible to draw a continuous line in the EMNZ region between the input port and the output port. This ensures that there is a channel, even if infinitesimally small, to support the transport of energy.
“Static optics,” supercoupling, and eigenmodes
In classical electrodynamics, the coupling of electric and magnetic fields via the time-harmonic source-free Maxwell curl equations—∇ × H = –iωε0εE and ∇ × E = iωμ0μH—is central, as it leads to our understanding of electromagnetic fields and waves as a single entity. Yet Richard Ziolkowski of the University of Arizona has noted that the presence of epsilon-and-mu-near-zero (EMNZ) media challenge this very concept. Within such media, electric and magnetic fields become irrotational (∇ × H and ∇ × E both approximate zero), which effectively decouples electricity and magnetism. Consequently, EMNZ supports decoupled electric and magnetic fields with static spatial distributions, harmonically oscillating in time at angular frequency ω.
Static optics and supercoupling.
This unconventional field dynamics, which we refer to as “static optics,” is one reason for various exotic phenomena observed in EMNZ media. One such phenomenon is supercoupling and its continuous-path requirement. If both relative permeability and relative permittivity are simultaneously scaled by a factor p (that is, if ε’ = pε and μ’ = pμ), then the fields found as the solution to the time-harmonic, source-free, Maxwell Equations are identical to those obtained when the frequency is scaled by the same factor, since –iωε0(pε)E = –i(pω)ε0εE and iωμ0(pμ)H = i(pω)μ0μH.
This explains intuitively how the effective wavelength is enlarged compared with an obstacle as the relative permittivity and permeability approach zero, resulting in zero reflection and “supercoupling” through the obstacle. But this characteristic of EMNZ materials falls more rigorously out of the general notion of static optics: Because the electric and magnetic fields become irrotational as the permittivity and permeability approach zero, the only possible way to enforce a zero circulation of the fields in a two-port structure, as required by Maxwell’s equations, is in the case of complete transmission. Supercoupling, which seems exotic, is mathematically required in an EMNZ world.
Static optics and bound eigenmodes.
The field dynamics of static optics also imply an effective decoupling between temporal and spatial field variations. In simple terms, the temporal variations, represented by frequency f, are intrinsically related to the spatial variations, represented by wavelength λ, via the medium’s phase velocity, f λ = (εμ)½. However, this connection is somewhat “loosened” in the presence of media with near-zero parameters, resulting in an approximate decoupling of temporal and spatial features. Although the phase velocity can attain large values, the temporal dispersion of such media ensures that the group velocity always stays less than the vacuum speed of light.
The decoupling of spatial and temporal variations in the ZI regime explains the ability of ENZ materials to support bound eigenmodes. In essence, since ε ≈ 0, the extended Ampère-Maxwell law ∇ × H = –iωε0εE supports a nonzero time-harmonic electric field, ωE ≠ 0, even in the absence of a magnetic field, H = 0. Because this field must be irrotational, the electric field spatial distribution can be written as the gradient of a scalar potential, E(r) = –∇V(r). Consequently, if the cavity supports such a nontrivial “electrostatic” field distribution that varies monochromatically with time, the cavity also supports an eigenmode at the ENZ frequency—independent of the geometry of its external boundary.
The effect works because, as the relative permittivity and permeability both approach zero, the effective wavelength of the light dramatically increases, and the physical obstacle of the deformation shrinks to an “electromagnetic point.” That results in zero reflection and “supercoupling” through the obstacle—and, thus, the ZI platform allows light to actually be transmitted through a deformable channel. (For more on the math behind EMNZ effects, see the sidebar at right “ ‘Static optics,’ supercoupling, and eigenmodes.”)
This unusual, geometry-invariant “tunneling” effect has obvious practical applications for waveguide systems in complex “flexible” environments. On the more theoretical side, it’s likely that complex light-matter interactions will take place for classical bodies and small quantum systems embedded in such structures, which could be inspected by analyzing their impact on the light transmitted through the channel. These might include, for example, slow light and nonlinear phenomena such as second- and third-harmonic generation; or collective spontaneous-emission effects for quantum emitters embedded within, or in proximity of, the deformed section. Moreover, work on the long-range interaction and consequent entanglement between quantum emitters coupled to these EMNZ and ZI channels may enhance and complement waveguide setups for quantum electrodynamics (QED), which are currently receiving a great deal of attention as a platform for entanglement generation and quantum information processing.
Geometry-invariant resonators: Trapping light
ZI platforms also challenge another conventional assumption: the supposed impossibility of localizing and trapping light within an open cavity.
In general, light diffracts, expands and propagates, and it cannot be stored within a cavity open to an unbounded environment. Even if we manage somehow to concentrate light within a small region at a given time, it will evolve to disperse and expand away from that region, ultimately forming outgoing waves with ever-smaller energy densities. Admittedly, the process can be slowed using optical cavities with high quality factors, and plasmonic nanoparticles and nanoantennas can provide subwavelength field concentrations. But a finite amount of radiation loss is always present, and none of these approaches provides a complete solution to the conceptual problem of localizing light in open cavities.
ZI materials, however, offer an unusual route around this problem. Specifically, as the research teams of Mario Silveirinha (University of Lisbon, Portugal) and Andrea Alù (University of Texas at Austin, USA) have independently shown, an open ENZ spherical shell can support bound eigenmodes—solutions to Maxwell’s equations that are confined to a region of space, even if that region opens to an unbounded background. These solutions thus represent a theoretically perfect confinement of light in an open cavity.
Our group has generalized this concept, demonstrating theoretically that the same effect actually takes place independent of the geometry of the cavity’s external boundary. This extends the concept’s potential applicability beyond symmetrical configurations, and, more importantly, introduces the notion of geometry-invariant resonant cavities—closed or open resonators supporting eigenmodes whose eigenfrequencies do not vary with variations of the external boundary deformations.
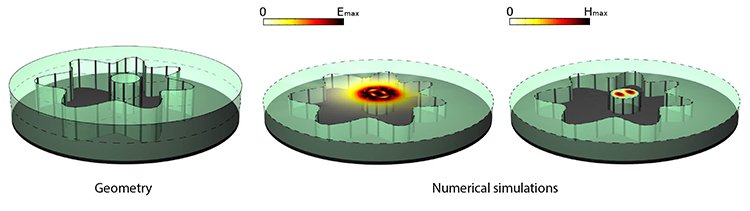
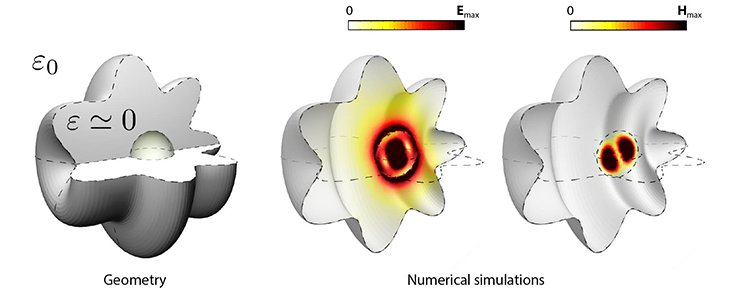 Bound eigenmodes in an open cavity: Numerical simulations show that an arbitrarily shaped ENZ body with an open boundary, containing a spherical dielectric “defect,” can support bound eigenmodes—solutions to Maxwell’s equations that are confined to a region of space even though the cavity is open. The monochromatic electric field in the ENZ shell is spatially “electrostatic,” with a zero magnetic field, but both fields are present in the dielectric defect.
Bound eigenmodes in an open cavity: Numerical simulations show that an arbitrarily shaped ENZ body with an open boundary, containing a spherical dielectric “defect,” can support bound eigenmodes—solutions to Maxwell’s equations that are confined to a region of space even though the cavity is open. The monochromatic electric field in the ENZ shell is spatially “electrostatic,” with a zero magnetic field, but both fields are present in the dielectric defect.
This effect is not an instance of topological photonics, and is not tied in any way to the topology of the cavity; we could dramatically change the topology by making holes in the cavity, yet it would still support an eigenmode at the ENZ frequency. Instead, the bound eigenmodes are in a sense analogous to the quantum-mechanical concept of a bound state in the continuum. More concretely, the anomalous geometry invariance lies in the decoupling of spatial and temporal field variations in the ZI regime.
Flexible, high-Q cavities?
In a conventional cavity, the field distribution of a resonant mode can be found as the superposition of multiple wave reflections from the cavity boundaries. This interference process requires precise phase accumulation conditions that strongly depend on the geometry of the external boundary. For example, the resonance frequency typically increases as the cavity’s size decreases. By contrast, no phase variation exists in the ZI regime—and, as with electrostatic fields, the spatial distribution of the fields is determined by the accumulation of charge on the boundaries. Therefore, the mechanisms that construct the fields in a ZI cavity obey qualitatively different physics than those in conventional cavities.
One remarkable consequence is that there exist cavities whose resonance frequency is pinned to the ZI or plasma frequency, and it is independent of the geometry of their external boundary. This new class of resonant cavities could both meet multiple practical applications and trigger fundamental research. For instance, high-Q cavities that experience no detuning when their external boundaries deform are an obvious fit in the world of flexible photonics, and could lead to deformable, stretchable resonant optical devices. Moreover, since radiation losses are reduced for a bound eigenmode, these cavities might even potentially be considered in the design of zero-threshold lasers. And Silveirinha of the University of Lisbon has shown that these cavities could be accessed from the outside by using nonlinear media—which creates the intriguing possibility of storing light within them.
From a more fundamental perspective, the possibility of dynamically deforming an optical cavity without introducing detuning might unveil new phenomena in classical and quantum optics. A photonic state initially stored in the cavity could experience anomalous dynamics as the external boundary of the cavity changes in time. If the cavity contained one or more quantum emitters, even more complex phenomena might be observed—the excitation of dynamic light-matter bound states, for example, or engineered spontaneous emission.
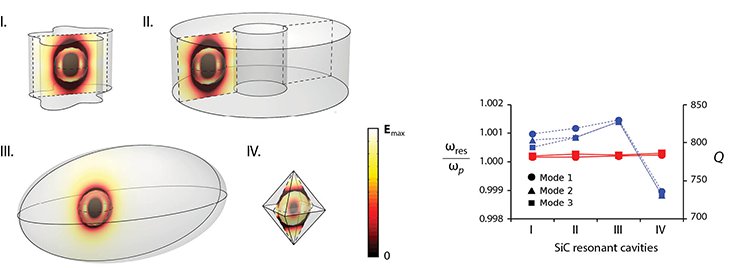 Different cavities, same frequency: Numerical simulations for four different modeled geometries of silicon-carbide (SiC) resonant cavities, each containing a spherical silicon particle (left), show three degenerate eigenmodes with similar resonance eigenfrequencies (red plot at right), but different quality factors (blue plot). SiC was modeled following Kim et al., Optica 3, 339 (2016).
Different cavities, same frequency: Numerical simulations for four different modeled geometries of silicon-carbide (SiC) resonant cavities, each containing a spherical silicon particle (left), show three degenerate eigenmodes with similar resonance eigenfrequencies (red plot at right), but different quality factors (blue plot). SiC was modeled following Kim et al., Optica 3, 339 (2016).
Implementing ZI platforms
Implementing these concepts, and exploiting them in new technologies, will depend on finding appropriate materials and structures—in particular, low-loss ENZ and EMNZ media. A variety of research groups in materials science and engineering have made strong progress, providing relatively low-loss ENZ responses at mid-infrared frequencies (for example, in silicon carbide) and near-infrared frequencies (for example, using aluminum-doped zinc oxide).
Synthetic implementations of ZI platforms have been successful, too. As noted in early works on artificial dielectrics, structural dispersion in waveguides and wire meshes behaves like an artificial plasma—that is, an ENZ medium. This methodology, further developed, has been used to measure and validate some of the most exotic scattering properties of ENZ and EMNZ materials, including supercoupling.
Alternatively, arrays of dielectric particles can be arranged to construct photonic crystals and metamaterials with ZI responses. This route to ZI platforms has also been experimentally demonstrated by X. Huang et al. and P. Moitra et al., and even integrated on a chip by A. Y. Li et al., providing a convenient and particularly low-loss pathway to scale these concepts to higher frequencies.
In our group, we have recently explored a very different path that enables the synthesis of ZI platforms in complex scattering scenarios, such as supercoupling and geometry-invariant bound eigenmodes. Complementing earlier pioneering works on artificial dielectrics, this approach relies on structural dispersion in waveguides supporting a TE10 waveguide mode with a Drude-like dispersion profile, and, crucially, on suppression of unwanted modes, achieved by thin wires placed at the interfaces between different media. This method allows the modeling and effective synthesis of complex scattering scenarios with multiple, arbitrarily shaped surfaces.
We have successfully exploited this methodology to imitate several plasmonic features within a waveguide filled with conventional dielectrics with positive permittivity, including surface plasmon polaritons, local plasmonic resonances, cloaking and ENZ supercoupling. However, this is a completely general technique that could be extrapolated to virtually any plasmonic phenomenon. Among other possibilities, the technique could facilitate implementation of the aforementioned geometry-invariant supercoupling and bound eigenmode effects, which involve the interaction with an intricate boundary.
 A synthetic route to open ENZ cavities: A parallel-plate waveguide with TE10 mode, and with thin shorting wires to prevent mode coupling, exhibits features and field distributions that one would expect in an open ENZ shell, including the excitation of a bound eigenmode in the open cavity and a spatially “electrostatic” time-harmonic field distribution in the shell region.
A synthetic route to open ENZ cavities: A parallel-plate waveguide with TE10 mode, and with thin shorting wires to prevent mode coupling, exhibits features and field distributions that one would expect in an open ENZ shell, including the excitation of a bound eigenmode in the open cavity and a spatially “electrostatic” time-harmonic field distribution in the shell region.
Even more important, the technique recovers not only the macroscopic, global response of the systems, such as the excitation of a bound eigenmode, but also can replicate the spatial distributions of the electric and magnetic fields at a local level. Such synthetic implementations of a ZI platform could thus replicate the response of an effective medium even for localized light-matter interactions—the radiation of a classical source in the presence of these ZI structures, for example, or the interaction and entanglement of quantum emitters located in the vicinity of such a synthesized ZI platform.
Stretching the possibilities
In the ZI regime, light defies some of our usual intuitions regarding wave dynamics. The existence of physical quantities that become invariant under geometrical deformations opens the possibility of investigating light-matter interactions within a platform in which concepts as basic as geometry play a qualitatively different role. And, even if low-loss ZI media at the frequency of interest are not available in nature, a variety of ENZ and EMNZ platforms can be developed to engineer them in practice, ranging from all-dielectric photonic crystals and metamaterials to synthetic implementations based on structural dispersion and textured surfaces.
Some of these engineered implementations can re-create complex scattering scenarios, opening the way to investigate the response of ZI media with intricate boundaries. The geometry-independent characteristics of the ZI regime could put practical deformable and stretchable devices within reach—and lay down a path for new, fundamental research in wave dynamics and quantum optics.
Iñigo Liberal and Nader Engheta are with the Department of Electrical and Systems Engineering, University of Pennsylvania, Philadelphia, Pa., USA.
References and Resources
-
W. Rotman. “Plasma simulation by artificial dielectrics and parallel-plate media,” IRE Trans. Antennas. Propag. 10, 82 (1962).
-
R.W. Ziolkowski. “Propagation in and scattering from a matched metamaterial having a zero index of refraction,” Phys. Rev. E 70, 046608 (2004).
-
M.G. Silveirinha and N. Engheta. “Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near-zero materials,” Phys. Rev. Lett. 97, 157403 (2006).
-
F. Haldane and S. Raghu. “Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry,” Phys. Rev. Lett. 100, 013904 (2008).
-
X. Huang et al. “Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials,” Nat. Mater. 10, 582 (2011).
-
R. Maas et al. “Experimental realization of an epsilon-near-zero metamaterial at visible wavelengths,” Nat. Photon. 7, 907 (2013).
-
P. Moitra et al. “Realization of an all-dielectric zero-index optical metamaterial,” Nat. Photon. 7, 791 (2013).
-
A.M. Mahmoud and N. Engheta. “Wave-matter interactions in epsilon-and-mu-near-zero structures,” Nat. Commun. 5, 5638 (2014).
-
M.G. Silveirinha. “Trapping light in open plasmonic nanostructures,” Phys. Rev. A 89, 023813 (2014).
-
F. Monticone and A. Alù. “Embedded photonic eigenvalues in 3D nanostructures,” Phys. Rev. Lett. 112, 213903 (2014).
-
N. Kinsey et al. “Epsilon-near-zero Al-doped ZnO for ultrafast switching at telecom wavelengths,” Optica 2, 616 (2015).
-
S. Lannebère and M.G. Silveirinha. “Optical meta-atom for localization of light with quantized energy,” Nat. Commun. 6, 8766 (2015).
-
A.Y. Li et al. “On-chip zero-index metamaterials,” Nat. Photon. 9, 738 (2015).
-
I. Liberal and N. Engheta. “Nonradiating and radiating modes excited in open epsilon-near-zero cavities,” http://arxiv.org/abs/1512.01092 (2015).
-
C. Della Giovampaola and N. Engheta. “Plasmonics without negative dielectrics,” Phys. Rev. B 93, 195152 (2016).
-
I. Liberal et al. “Geometry-invariant resonant cavities,” Nat. Commun. 7, 10989 (2016).
