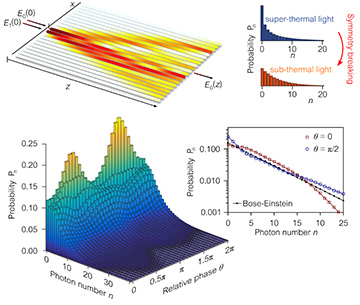
 Top left: A disordered photonic lattice of randomly coupled waveguides is coherently excited at two neighboring lattice sites and the photon-number distribution from the central lattice point is measured. Top right: When a relative phase of π/2 is inserted between the input coherent fields at two neighboring lattice points, the output field exhibits super-thermal statistics. Changing the relative phase breaks the excitation symmetry, resulting in sub-thermal statistics. Bottom: The photon-number distribution can be controlled deterministically by tuning the relative phase at the input.
Top left: A disordered photonic lattice of randomly coupled waveguides is coherently excited at two neighboring lattice sites and the photon-number distribution from the central lattice point is measured. Top right: When a relative phase of π/2 is inserted between the input coherent fields at two neighboring lattice points, the output field exhibits super-thermal statistics. Changing the relative phase breaks the excitation symmetry, resulting in sub-thermal statistics. Bottom: The photon-number distribution can be controlled deterministically by tuning the relative phase at the input.
The central limit theorem dictates that adding a large number of independent random variables tends toward a bell-shaped distribution. Thus, upon ensemble averaging, coherent light traversing a disordered medium should gradually become random in amplitude and phase, with Gaussian statistics for both field quadratures—that is, chaotic or thermal light. Such light exhibits Bose-Einstein photon-number statistics, with the photon bunching associated with those statistics. Conditions for the central limit theorem are not always met, however, and deviations from Bose-Einstein statistics do occur, depending on the disorder level. Given that, for a fixed disordered medium, can the statistics of the transmitted photons be altered deterministically by only changing the spatial distribution of the incident coherent light itself?
We have theoretically predicted1 and experimentally demonstrated2,3 that deterministic sculpting of the coherent field entering certain disordered photonic lattices endowed with so-called off-diagonal disorder—typically realized in arrays of identical but randomly coupled waveguides—can help tune the photon-number distribution. The result is light with higher or lower uncertainties than those of chaotic light, thereby allowing control of the bunching of photons exiting the structure.
The underlying mechanism enabling this control over photon bunching stems from a disorder-immune symmetry in the spatial eigenmodes of the disordered photonic lattices. That symmetry leads these eigenmodes to appear in pairs, with eigenvalues having equal amplitude but opposite signs. When a relative phase of π/2 is introduced between the coherent fields coupled into two neighboring lattice sites, the eigenmode pairs are symmetrically excited, leading to a field (with super-thermal statistics) that is random in amplitude but has discrete phase values.4 Photon bunching is boosted in this case, even though the mean photon number remains fixed. Breaking the excitation symmetry by changing the relative phase at the input (to 0 for example) results in a random field both in amplitude and phase (and, hence, sub-thermal statistics); this deterministically reduces the photon bunching and controllably changes the photon-number distribution.
We believe these results may pave the way to on-chip integrated chaotic light sources with controllable photon bunching, for speckle-free biomedical imaging.
Researchers
H. Esat Kondakci, Ayman F. Abouraddy and Bahaa E. Saleh, CREOL, the College of Optics & Photonics, University of Central Florida, Orlando, Fla., USA
References
1. H.E. Kondakci et al. Nat. Phys. 11, 930 (2015).
2. H.E. Kondakci et al. Optica 3, 477 (2016).
3. H.E. Kondakci et al. APL Photonics 2, 71301 (2017).
4. H.E. Kondakci et al. Sci. Rep. 7, 8948 (2017).
