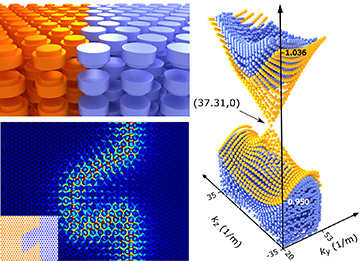
 Clockwise from top-left: 3-D all-dielectric photonic topological insulator; conical Dirac-like dispersion of topological surface states; field distribution of the surface modes propagating without reflection across the domain wall, with the sequence of sharp bends depicted in inset. [Reprinted by permission from Macmillan Publishers Ltd., Nat. Photon. 11, 130 (2017), ©2017]
Clockwise from top-left: 3-D all-dielectric photonic topological insulator; conical Dirac-like dispersion of topological surface states; field distribution of the surface modes propagating without reflection across the domain wall, with the sequence of sharp bends depicted in inset. [Reprinted by permission from Macmillan Publishers Ltd., Nat. Photon. 11, 130 (2017), ©2017]
Topological materials not only are revolutionizing our views on solid-state materials but also promise unprecedented advances in technology. In recent years, it has become clear that topological phases are not limited to fermionic systems, but can also be found in classical systems, including photonic crystals and metamaterials.1 Early approaches to photonic topological order relied on ferrites to break time-reversal (TR) symmetry using a magnetic field. Such an approach is impractical at optical frequencies, however, owing to a lack of photonic magnetic materials with a strong magneto-optical response. That has led to an increased interest in systems in which TR symmetry is either preserved or is broken by a different means.2
Several successful theoretical designs and experimental implementations of topological states of light with TR symmetry have been reported, but these ideas have been restricted to 2-D topological states. Very recently, theoretical research on 3-D photonic topological states using magnetic ferrites has begun3—work that, while groundbreaking from a theoretical perspective, still suffers from the same limitations as 2-D counterparts using magnetic materials.
This year, we introduced a concept for all-dielectric 3-D photonic topological insulators that preserve TR symmetry and that thus avoid the limitations imposed by magnetic materials.4 By relying entirely on an all-dielectric platform5—which also avoids the undesirable effects of ohmic losses necessarily present in metallic and plasmonic structures—this concept can support 3-D topological order for light.
We believe that this proposal is fundamentally important, because it represents the first all-dielectric system reported thus far that exhibits 3-D topological order in a relatively simple, photonics-friendly platform. In addition, this platform offers (for the first time to our knowledge) the ability to emulate the 3-D Dirac equation (as opposed to the 2-D Dirac equation in graphene-like systems) and exotic states of relativistic fermions.
The finding also has significant potential for practical applications in optics. Indeed, it was demonstrated that the proposed, topologically nontrivial metamaterial supports helical electromagnetic excitations that can tolerate sharp bends and propagate without reflection. Electromagnetic radiation in the form of topological surface modes flows unimpeded along arbitrary contours defined by the synthetic gauge field, which points to applications in implementing of topologically robust, 3-D photonic circuitry.
Researchers
Alexey Slobozhanyuk, ITMO University, St. Petersburg, Russia
Yuri S. Kivshar, Australian National University, Canberra, Australia
Alexander B. Khanikaev, City College of the City University of New York, N.Y., USA
References
1. L. Lu et al. Nat. Photon. 8, 821 (2014).
2. K. Fang et al. Nat. Photon. 6, 782 (2012).
3. L. Lu et al. Nat. Phys. 12, 337 (2016).
4. A. Slobozhanyuk et al. Nat. Photon. 11, 130 (2017).
5. A. Kuznetsov et al. Science 354, aag2472 (2016).
Note: The authors wish to acknowledge support for this work by the Russian Science Foundation (grant no.16-19-10538).
