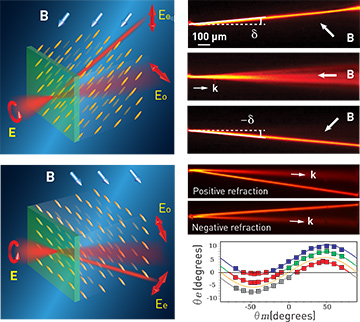
 Routing of self-trapped beam in liquid crystals by a magnetic field, B. Top left: Orientation of B determines orientation of rod-shaped NLC molecules, defining soliton trajectory. Top right: Photographs of e-polarized self-confined solitons at azimuthal angles of 90° (upper) and 270° (lower), as well as o-polarized diffracting beam (middle). Bottom: Tilting incident beam and magnetic-field direction leads to switching between positive and negative refraction of e-wave spatial soliton for an incidence angle of 3.1°. Chart at lower right shows refraction angle of e-beam (θe) versus azimuthal orientation of B (θm). Colors indicate incidence angles (blue, 7.4°; green, 3.1°; gray, –3°; yellow, 0°); red squares correspond to negative refraction.
Routing of self-trapped beam in liquid crystals by a magnetic field, B. Top left: Orientation of B determines orientation of rod-shaped NLC molecules, defining soliton trajectory. Top right: Photographs of e-polarized self-confined solitons at azimuthal angles of 90° (upper) and 270° (lower), as well as o-polarized diffracting beam (middle). Bottom: Tilting incident beam and magnetic-field direction leads to switching between positive and negative refraction of e-wave spatial soliton for an incidence angle of 3.1°. Chart at lower right shows refraction angle of e-beam (θe) versus azimuthal orientation of B (θm). Colors indicate incidence angles (blue, 7.4°; green, 3.1°; gray, –3°; yellow, 0°); red squares correspond to negative refraction.
The ability to create reconfigurable photonic circuits without prefabricated optical waveguides is just one possibility stemming from self-guided light beams, known as optical spatial solitons. Among the best nonlinear media for this are nematic liquid crystals (NLCs)—a unique material amenable to several applications, as it modifies its optical properties under external stimuli.
Most previous work has exploited the NLC reorientation response to light in thin samples in which the initial molecular distribution is defined by boundaries of a planar cell or an applied external voltage.1,2. This has confined NLC spatial solitons—nematicons—to propagating essentially within a plane, which has significantly limited their applications.
This year, we proposed a drastically simple approach to launch and direct stable solitons in bulk NLCs with an external magnetic field, effectively controlling their trajectories and the angular orientation of the self-induced waveguides.3 This allows us to achieve a fully 3-D manipulation of soliton trajectories in NLC.
We used circularly polarized beams yielding o- and e-components of equal powers. While the e-wave electric field Ee tends to align the NLC molecules along its own polarization, the external magnetic field B determines the background alignment; the stronger B, the higher the beam power required to produce an index change Δn for self-trapping.
When B is tilted with respect to z, the o-component propagates along the original direction (z) undergoing diffraction, while the e-field walks-off at angle δ and forms a nematicon via reorientational self-focusing (see figure). As B is rotated around z, the soliton follows this rotation. Moreover, by tilting the incident beam and the direction of the applied magnetic field B, the optical soliton can experience either positive or negative refraction.4
Thus, we demonstrated an approach to routing self-localized beams and light-induced waveguides in 3-D, without the usual limitations imposed by transverse boundary conditions. Such flexibility unveils rich scenarios for soliton-based optical circuits and reconfigurable photonic interconnects.
Researchers
Yana Izdebskaya and Vladlen Shvedov, The Australian National University, Canberra, Australia
Gaetano Assanto, University “Roma Tre,” Rome, Italy, and Tampere University of Technology, Tampere, Finland
Wieslaw Krolikowski, The Australian National University and Texas A&M University at Qatar, Doha, Qatar
References
1. G. Assanto et al. Opt. Photon. News 14(2), 44 (February 2003).
2. M. Peccianti et al. Nature 432, 733 (2004).
3. Y. V. Izdebskaya et al. Nat. Commun. 8, 14452 (2017).
4. V. G. Shvedov et al. Appl. Phys. Lett. 110, 091107 (2017).
