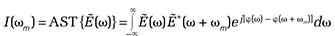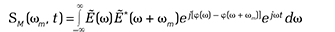Feature OPEN

The Anamorphic Stretch Transform: Putting the Squeeze on “Big Data”

Bahram Jalali and Mohammad H. Asghari

Coping with a deluge of digital information will require more efficient ways to capture, sample and store data. One new approach works by selectively “warping” the data to provide better resolution of the fine details—while still reducing total data size.

The world today is awash in digital data. It’s estimated that more than 2.5 exabytes (2.5 × 10¹⁸ bytes) of data were being churned out every day in 2012, with 90 percent of all of the world’s data created in just the last two years. The quintillions of bytes of “Big Data” collected by millions of networked sensors, and generated by users of smartphones and other networked devices, have spurred wide discussion of the opportunities to be mined from the data—and the challenge of properly analyzing it all.

But the Big Data problem isn’t limited to analytics; it also includes data capture, storage and transmission. In applications such as data communication, medicine and scientific research, communication signals and phenomena of interest occur on time scales too rapid and at throughputs too high to be sampled and digitized in real time.

Our group at the University of California, Los Angeles, which develops high-throughput, real-time instruments for science, medicine and engineering, has experienced this firsthand. The record throughput of instruments such as serial time-encoded amplified microscopes, MHz-frame-rate brightfield cameras, and ultra-high-frame-rate fluorescent cameras for biological imaging has enabled the discovery of optical rogue waves and the detection of cancer cells in blood with sensitivity of one cell in a million.

But these instruments also produce a data “firehose”—on the order of one trillion bits of data per second for some systems—that can overwhelm even the most advanced computers. And detecting rare events such as cancer cells in a flow requires that data be recorded continuously and for a long time, resulting in vast data sets.

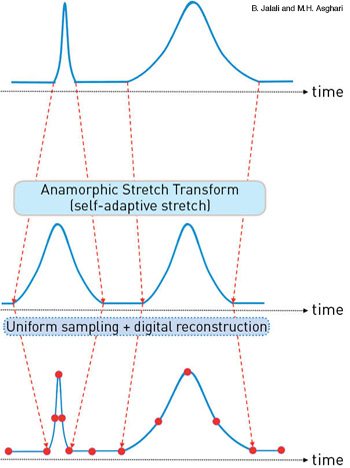Self-adaptive stretch: With AST, sharp features are stretched more than coarse features before uniform sampling. This makes for the most efficient use of limited available samples, and reduces the overall size of the digital data.

Dealing with such data loads requires new approaches to data capture and compression. We have developed such an approach: the Anamorphic Stretch Transform (AST), a new way of compressing digitized data by selectively stretching and warping the signal.

This operation emulates what happens to waves as they travel through physical media with specific dispersive or diffractive properties. It also evokes aspects of surrealism and the optical effects of anamorphism used in visual arts. This technique, with applications both in digitizing high-throughput analog signals and in compressing already digitized data, could offer one route to taming the capture, storage and transmission bottlenecks associated with Big Data.

The Nyquist dilemma

Much of the problem of capturing and handling Big Data lies in familiar constraints of analog-to-digital conversion. Conventional digitizers sample the analog signal uniformly at twice the highest frequency of the signal—the so-called Nyquist rate—to ensure that the sharpest features are adequately captured. Unfortunately, this oversamples frequency components below the Nyquist rate, which can make the total digital record far larger than it needs to be. And the Nyquist rate criterion limits the maximum frequency that can be captured to half of the digitizer’s sampling rate, a problem in dealing with increasingly fast, high-throughput data.

AST is a physics-based data compression technique that solves both problems. By reshaping the signal before sampling, and selectively stretching and warping sharp features in the data to allow them to be captured at a lower sampling rate, the transformation matches the signal’s bandwidth to the capabilities of the sensor and the digitizer.

At the same time, it compresses the time-bandwidth product (TBP)—the product of the record length and the bandwidth, which is the parameter that determines the total number of samples, and thus the digital data size, required to represent the original information in a non-lossy way. The result: Fast features that were previously beyond resolution can be properly captured, yet the total volume of digital data is reduced.

Anamorphism in Art

The Anamorphic Stretch Transform takes its name from the technique of anamorphism in graphic arts. Here, artists use transformations and warping in the spatial domain to fashion distorted perspectives of images for artistic effect—which can be reconstructed into their original form using curved mirrors, changes of perspective, or other techniques. One well-known form of anamorphism is cylindrical anamorphism, shown in the example above: The distorted design of the art on the plane surface is rolled up into the “real” image, a column, in the cylindrical mirror.

AST, by analogy, achieves its effectiveness by selectively stretching and warping a signal not in space, but in the frequency domain, and can similarly reconstruct the original signal through an inverse transformation. The selective warping in AST also spurs associations with surrealist art, such as Dali’s famous warped watches in “The Persistence of Memory,” evoked in the art below.

Stretching the features self-adaptively

At the heart of AST is the concept of self-adaptive stretch: By reshaping the actual input signal before uniform sampling, AST causes sharp features to be stretched more than coarse features. This feature-selective stretch means that more samples are allocated to sharp features in the data, where they are needed the most, and fewer to coarse features, where they are redundant.

In most situations involving digital data the number of available samples is limited, either by the resolution of the digitizer itself or by storage and transmission capacity. Feature-selective stretch allocates those limited available samples most efficiently, and reduces TBP when there is redundancy in the signal.

In analog-to-digital conversion, AST reshaping of the signal’s modulation envelope consists of two steps. First, the electric field is passed through a physical medium engineered to have specific dispersion or diffraction properties, and thereby to achieve feature-selective stretch in the input waveform. The second step is a nonlinear operation—in the case of temporal optical waveforms, the detection of the modulation envelope with a square-law detector. The data are then compressed by undersampling the reshaped waveform with uniformly spaced samples, at a frequency below that determined by the Nyquist rate of the original data.

Since it uses nonlinear dispersion to minimize the record length—i.e., the volume of data—AST can be also referred to as dispersive data compression for time domain applications and as diffractive data compression for images. Data compression via dispersion/diffraction is a new concept, and one that we believe has tremendous potential. It can also, as noted later, be implemented not only for analog-to-digital conversion, but as a data compression algorithm for information already captured digitally.

Engineering the right warp

In capturing fast optical signals for digitization, AST works by passing the analog data through a physical medium, with specific dispersion properties—in essence, a specific group delay function that preferentially stretches out sharp features for more detailed capture. But how do we engineer a medium that warps the signal in the right way? The answer lies in the math of the transformation—and in a very useful distribution function that falls out of that math.

Mathematics of AST

AST can be represented in frequency domain or time (space) domain. In its frequency domain representation, AST is defined as:

where ω is the carrier frequency and ω_mis the envelope modulation (sideband) frequency. Mathematically, AST is an autocorrelation function with an embedded kernel (the exponential term) that describes a frequency-dependent phase operation, φ(ω). Correct selection of φ(ω) allows the time-bandwidth product to be compressed or expanded. The mathematical tool for making that selection is the Stretched Modulation Distribution function, S_M:

where t denotes the time variable.

Mathematically, as shown in the sidebar on the right, AST constitutes a nonlinear transform that stretches and warps the input signal field spectrum, E(ω), to a warped intensity spectrum, I(ω_m). The output of the transform includes both amplitude and phase information, so the complex field of the reshaped input signal must also be measured. The time domain signal can then be fully reconstructed from the measured complex field.

The output of AST includes a frequency-dependent phase operation, φ(ω), the proper choice of which will determine whether the TBP is compressed or expanded. The challenge, of course, is to identify the type of phase operations that results in feature-selective stretch of the modulation envelope, which in turn enables us to engineer the right physical or digital filter to achieve the compression. To do this, we use the Stretched Modulation Distribution (S_M), a mathematical tool that describes both the record length and the modulation bandwidth after the signal is subjected to a given phase operation.

S_M is a 2-D function that unveils the signal’s modulation bandwidth and its dependence on the group delay, and thus can identify the proper kernel that reshapes the signal such that its TBP is compressed. It allows us to engineer the TBP of signal intensity (or brightness) though proper choice of the φ(ω) function—or, more precisely, its derivative, which maps to the group delay of the dispersive element.

The usefulness of S_M in engineering TBP compression can be seen by comparing the distribution for an arbitrary signal for a linear and a warped (nonlinear) group delay. A linear group delay compresses the bandwidth, but expands the record length, so TBP is not compressed; a nonlinear group delay results in bandwidth compression without significant increase in record length.

It turns out that for TBP compression, the group delay should be a sublinear function of frequency. One simple example that can achieve good TBP compression is the inverse tangent, dφ (ω)/dω = A • tan^–1 (B • ω). Here A and B are arbitrary real numbers, with the adjustable parameter B specifically related to the degree of anamorphism, or warp, imparted on the signal. (For time-bandwidth expansion and application to waveform generation from digitized data, the group delay should be a superlinear function of frequency.)

The process for unpacking the compressed digital signal consists of complex-field detection, followed by digital reconstruction at the receiver—the latter being simply inverse propagation through AST. The net result is that the envelope (intensity) bandwidth is reduced without proportional increase in time, and the TBP is compressed. Since the volume of digital data is proportional to the TBP of the analog signal, this operation reduces the digital data volume and addresses the Big Data problem in high-speed, real-time systems.

AST and other stretch transforms

The potential effectiveness of AST in the Big Data regime emerges in comparison with two other transforms—Time-Stretch Dispersive Fourier Transform (TS-DFT) and Time-Stretch Transform (TST)—that were also designed to enable faster analog-to-digital signal capture.

TS-DFT relies on linear group velocity dispersion to perform time dilation and Fourier transformation. It enables measurement of single-shot spectra of optical pulses at high repetition rates, offers a powerful method for real-time high-throughput spectroscopy and imaging at high repetition rate, and led to the discovery of optical rogue waves. However, it does not provide information about the signal in the time domain or its spectral phase profile. TST combines this technique with complex-field detection and is capable of providing the single-shot spectrum and the temporal profile.

Both of these techniques, however, as well as temporal imaging, conserve the TBP of the input signal, and thus do not reduce the total data volume. AST, by contrast, engineers the time-bandwidth (or space-bandwidth) product of waveforms and also provides complex-field information in both the time and spectral domains in real time. By compressing the TBP, it reduces the record length and hence digital data size.

Compressing analog data

For temporal optical waveforms, AST can use elements with engineered group velocity dispersion, such as chirped fiber Bragg gratings, chromo-modal dispersion or free-space gratings, to perform the nonlinear group delay filter operation. Using a fiber grating with the proper sublinear group delay profile, THz-bandwidth optical pulses, carrying single-shot spectrum or imaging information, can be compressed to GHz-bandwidth temporal waveforms that can be digitized in real-time. At the same time, the temporal duration and hence the digital data size are reduced.

In experimental demonstrations of AST using a fiber Bragg grating with customized chirp profile, we achieved a 2.7-fold reduction in TBP, and thus in digital data size, in capturing and sampling an optical signal relative to TST techniques. For recovery of the complex field to decompress the data, we used the Stereopsis-inspired Time-stretched Amplified Real-time Spectrometer (STARS) method, an approach to optical signal phase recovery based on two intensity (envelope) measurements and inspired by stereopsis reconstruction is human eyes. (Other phase recovery techniques can also be used.)

A digital implementation of AST, coupled with standard JPEG compression, accomplishes 56-fold reduction in data size (right), without the loss of information entailed by using JPEG alone (left).

Toward all-digital implementations

As the example above suggests, AST can enable a conventional digitizer to capture fast temporal features that might otherwise be beyond its bandwidth, while reducing the total digital data size by compressing the TBP of the signal modulation. This analog compression is achieved in an open-loop fashion, without prior knowledge of the input waveform, and thus can address one aspect of the Big Data problem. But Big Data also raises issues about the storage and communication of the exabytes of data already in digital form, such as digital images. AST can also help address these challenges, through implementation of this analog system as a digital data-compression algorithm.

Implementing a version of AST for compression of digital data involves creating a compression algorithm based on a discrete approximation of the AST equations, using those equations to develop parameters for a digital transformation (analogous to the physical propagation through a warped dispersive or diffractive element), and passing an already captured and digitized signal through the compression algorithm. This would achieve the same kind of compression by allowing resampling of the selectively “warped” digital signal at a lower frequency, thereby allowing compression for storage and transmission, in the same way that the analog transform allows compression for actual data capture and analog-to-digital conversion.

We have used such an all-digital implementation to achieve significant (56-fold) compression in digital images, without the distortion implicit in common lossy compression algorithms such as JPEG. The example highlights AST’s potential as one part of the solution of the Big Data quandary.

Bahram Jalali is professor, Northrop Grumman Endowed Chair, and Mohammad H. Asghari is a postdoctoral fellow in the Electrical Engineering Department at the University of California, Los Angeles (UCLA), U.S.A. Jalali has joint appointments in the Biomedical Engineering Department, California NanoSystems Institute and the UCLA School of Medicine Department of Surgery.

References and Resources

M.H. Asghari and B. Jalali. “Anamorphic transformation and its application to time-bandwidth compression,” Appl. Opt. 52, 6735 (2013).
M.H. Asghari and B. Jalali. “Demonstration of analog time-bandwidth compression using anamorphic stretch transform,” Frontiers in Optics 2013, paper FW6A.2, Orlando, Fla.
M.H. Asghari and B. Jalali. “Image compression using the feature-selective stretch transform,” IEEE International Symposium on Signal Processing and Information Technology, paper S.B2.4, Athens, Greece.
B. Jalali and M.H. Asghari. U.S. Patent Applications 61/746,244 (2012).
K. Goda and B. Jalali. “Dispersive Fourier transformation for fast continuous single-shot measurements,” Nat. Photon. 7, 102 (2013).

Publish Date: 01 February 2014

ADVERTISEMENT