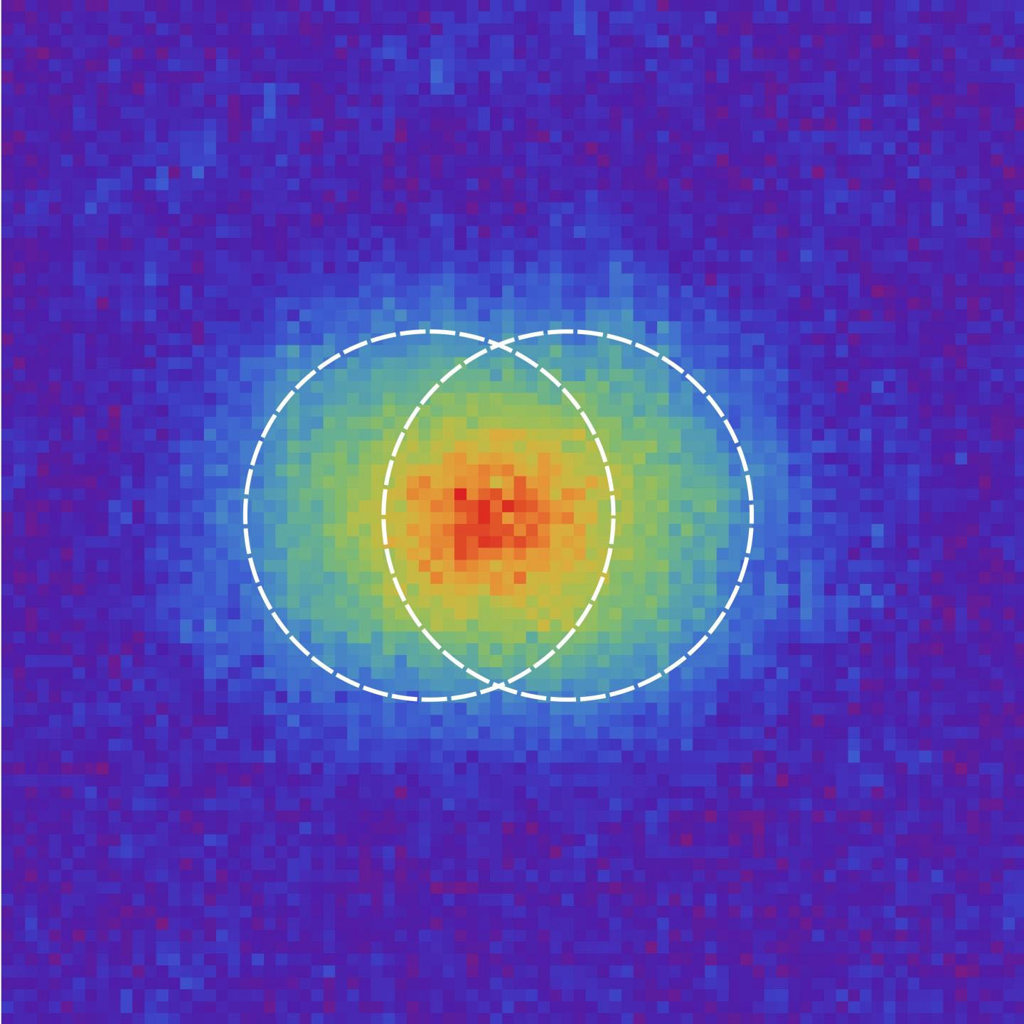
Two points separated by Rayleigh’s limit, as observed during the experiments at the Universidad Complutense de Madrid. [Image: Martin Paúr, Palacký University, Czech Republic]
Scientists working with images are constantly bumping against Rayleigh’s criterion for the minimum separation of two distinguishable points of light. A team of European scientists using information theory now claims to have developed an imaging method that surpasses the traditional resolution limit (Optica, doi:10.1364/OPTICA.3.001144)
The researchers used the notion of the quantum Cramér-Rao lower bound, which places limits on the variance of the estimators of certain parameters. The team set up and tested a measurement scheme that attains this kind of lower bound for Gaussian and sinc point spread functions.
Inspired research
Luis L. Sanchez-Soto, a quantum optics professor at Universidad Complutense de Madrid, Spain, got the original idea of examining the resolution limit from the standpoint of information theory when he attended a presentation by Mankei Tsang and his colleagues at the National University of Singapore. The Tsang group presented its new method (doi:10.1103/PhysRevX.6.031033) for using linear optics and photon counting to estimate the separation of two incoherent point sources from the far field. “I immediately reformulated his notion into a quantum language and asked my colleagues in Olomouc, Czech Republic, (the location of Palacký University) to perform the experiment, since they have a long tradition in the kind of optics needed for the implementation I devised.”
The team’s experiment consisted of two incoherent point sources of light imaged by a low-aperture lens and detected by an electron-multiplying CCD. Each experimental measurement, the authors wrote, “consists of two-photon counts detected from the Fourier spectrum points representing spatial frequencies connected with the reference waves.”
Counterintuitive results
“At the beginning, the experimentalists doubted the conclusions from my calculations,” says Sanchez-Soto. “The idea that, when using a complete set of measurements, the separation between two points can be resolved with arbitrary precision was very counterintuitive.” The idea of the Rayleigh criterion is correct hold only for “intensity” detection—which discards much of the information from the wave. “All the phase information is killed,” he adds.
Three other research collaborations—two in Canada and one in Singapore—have been pursuing the same line of research. A.I. Lvovsky’s group at the University of Calgary, Canada, just published its work on sub-Rayleigh precision via heterodyne detection in a higher-order local oscillation mode (doi:10.1364/OPTICA.3.001148).
Sanchez-Soto says he and his collaborators are now trying to generalize their theory to point sources with some arbitrary degree of coherence since Rayleigh’s criterion applies strictly to incoherent sources. The researchers are also working on practical ways to implement the technique.
