 A diffuser is attached to a gradient-index optic. The diffuser replaces the tube lens in a miniature microscope, adding 3D capability and shrinking the device. [Courtesy of N. Antipa]
A diffuser is attached to a gradient-index optic. The diffuser replaces the tube lens in a miniature microscope, adding 3D capability and shrinking the device. [Courtesy of N. Antipa]
 Vivek Boominathan (left) and Jesse Adams set up an experiment with FlatScope, a fingernail-sized lensless camera configured for use as a fluorescent microscope. FlatScope is able to capture 3D data and produce images from anywhere within the field of view. [Jeff Fitlow/Rice University]
Vivek Boominathan (left) and Jesse Adams set up an experiment with FlatScope, a fingernail-sized lensless camera configured for use as a fluorescent microscope. FlatScope is able to capture 3D data and produce images from anywhere within the field of view. [Jeff Fitlow/Rice University]
Traditional lens design aims primarily to create a sharp, bright image in the right place, so that a film or diode array can record a 2D image. High-quality lenses generally require many elements to achieve bright, aberration-free imaging. Recently, some aberration correction has moved out of the optical domain and into digital postprocessing, simplifying the optical designs. Lenses built around digital aberration compensation perform better and require fewer elements than classical lens designs, but until recently have chiefly been limited to 2D imaging.
Mask-based lensless cameras take this approach to an extreme, replacing the entire lens assembly with a single custom optic—a “mask”—that’s placed atop a digital sensor. For these cameras, the measurements are not image-like, requiring an algorithm to reconstruct the final image. Lensless cameras are gaining popularity within computational-imaging research not only for their compact form factors, but also because they efficiently capture extra dimensions about the scene such as depth, time or spectrum.
Lensless imaging has its roots in image capture at extreme wavelengths, where refractive optics are impractical or even impossible.
Pinhole-camera roots
Lensless imaging has its roots in image capture at extreme wavelengths—for example, X-rays and gamma rays—where refractive optics are impractical or even impossible. Without the possibility of focusing radiation to tight spots, the only alternative was patterned absorption. Unfortunately, pinhole cameras, the earliest absorption-only cameras, suffered from a poor flux–resolution tradeoff—that is, a larger pinhole increases flux but blurs the image.
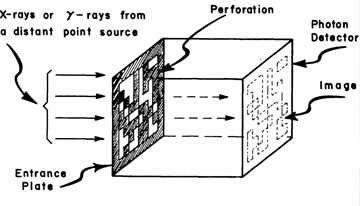 One of the earliest lensless imaging designs employed a randomly perforated mask to image X-ray or gamma ray sources with an unprecedented signal-to-noise ratio (SNR). [R.H. Dicke, Astrophys. J., 153, L101 (1968). © AAS; reproduced with permission]
One of the earliest lensless imaging designs employed a randomly perforated mask to image X-ray or gamma ray sources with an unprecedented signal-to-noise ratio (SNR). [R.H. Dicke, Astrophys. J., 153, L101 (1968). © AAS; reproduced with permission]
Pioneers in this space, J.G. Ables and Robert H. Dicke, each independently realized in the 1960s that this tradeoff could be broken using an array of many small pinholes carefully placed in relation to each other. The flux scaled with the number of openings, but the resolution was limited by the size of each individual pinhole. Imaging was possible because the pinhole array—called a mask, coded aperture or entrance plate—imprinted the mask pattern onto each incident beam, creating a uniquely identifiable measurement from any distant point source.
There were two major drawbacks to this design, however. First, images of multiple sources could only be recovered by computationally demixing the overlapping mask patterns. Second, this demixing problem became increasingly difficult for more complex scenes consisting of a large number of high-dynamic-range scene points. This object-dependent performance limited the quality of early coded-aperture cameras.
Modern digital sensors and algorithms have made the limitations of early coded-aperture cameras far easier to overcome. Now, the promise of extremely compact form factors and the ubiquity of computing have made lensless cameras an attractive design form across the electromagnetic spectrum.
Mask, sensor, algorithm
Whereas lens-based cameras project an image directly on the sensor, the mask in a lensless camera imprints a unique code on incident beams. A well-designed mask will create a unique pattern for every possible scene point that is high contrast and contains sharp features. When imaging a naturally illuminated scene, the mask pattern created by each scene point will add linearly on the sensor. With explicit knowledge of every possible mask pattern from across the field of view (FoV), the overlapping patterns can then be demixed by solving an inverse problem.
As with the earliest instances, the building blocks of lensless cameras today still comprise a coding mask, a digital sensor and a reconstruction algorithm. The key developments have been in engineering the individual components and in a greater understanding of the interactions between them. Codesigning all three components leads to cameras with unique form factors and imaging properties, such as capturing extra dimensions and increasing depth of field and FoV.
Coded-aperture cameras for extreme wavelengths used amplitude masks out of necessity. Many early optical lensless cameras, inspired by coded aperture, used amplitude masks as well. But, while easy to fabricate, these masks block 50% or more of incident light, and are limited in the possible point spread functions (PSFs) they can produce.
Phase-only masks offer an attractive alternative in optical wavelengths. These masks code incident wavefronts by introducing a phase modulation, leading to a high-contrast pattern downstream on the sensor. Compared with amplitude masks, phase masks significantly increase light efficiency and are more flexible in the range of coding patterns they can generate.
Thanks to new optical fabrication technology, complicated masks are now easier to fabricate, and with the advent of high-quality freeform and diffractive optic fabrication, customized phase optics are available at reasonable cost. For prototyping lensless cameras, 3D printing has reached quality levels that enable researchers to quickly generate customized phase masks. Advances in nanophotonics and 3D gradient-index optics, meanwhile, offer exciting new design spaces and capabilities not possible with a conventional phase surface.
 Lensless cameras like the DiffuserCam, demonstrated in 2018, consist of a diffuser atop a digital sensor, which records measurements that are reconstructed into a final image. [N. Antipa et al. Optica, 5, 1 (2018)]
Lensless cameras like the DiffuserCam, demonstrated in 2018, consist of a diffuser atop a digital sensor, which records measurements that are reconstructed into a final image. [N. Antipa et al. Optica, 5, 1 (2018)]
 Modern lensless systems like the “FlatScope” microscope objective are smaller than one’s fingernail. [J. Adams and V. Boominathan]
Modern lensless systems like the “FlatScope” microscope objective are smaller than one’s fingernail. [J. Adams and V. Boominathan]
Computational advances
In a lensless camera, the information from each scene point is distributed across multiple sensor pixels, requiring an algorithm to form the final image. Early algorithms for lensless cameras, limited by available computing resources, typically used correlation-based matched-filtering approaches, which needed only one or two Fourier transforms. This worked for sparse scenes but performed poorly in more complex, denser ones.
Contemporary algorithms use inverse-problem or machine-learning approaches to achieve far superior image quality. Inverse problems formulate image recovery as an optimization problem. These frameworks use an optical model for the camera hardware to estimate the scene from the sensor measurements. By using this formulation, designers can leverage decades of work on efficiently solving inverse problems. Optimization-based techniques also offer the ability to enforce a priori knowledge about the object being imaged. This can take many forms, including sparsity-based priors and image denoisers, which help compensate for the inherent object-dependent performance of lensless cameras.
Data-driven machine-learning approaches can achieve order-of-magnitude speed improvements at image qualities comparable to or better than those with optimization methods. Such methods can empirically learn highly accurate details of the optical system that would be too complex to capture with simple optical models. Also, for lensless cameras aimed at specific classes of images, data-driven approaches can learn stronger scene priors. These benefits, however, require extensive data and pre-training of the image reconstruction. This is an active area of research that could potentially reduce lensless-camera image reconstruction complexity to levels useful in mobile or Internet of Things applications, where the smaller camera size would matter most.
These approaches together point to a critical limitation of current lensless cameras: All depend on exhaustive pre-calibration and a stable system configuration to recover the image. If, “in the wild,” optics become damaged, displaced or dirty, the system model loses accuracy, and image-recovery algorithm results become unpredictable. In practice, optimization-based approaches can withstand changes to the system, but a solid understanding of sensitivity to shifting optics and their effect on overall image quality is still lacking.
While the anatomy of lensless cameras is largely unchanged from 50 years ago, our understanding of the interactions between the mask, sensor and algorithm has evolved.
Codesign and compressed sensing
While the anatomy of lensless cameras is largely unchanged from 50 years ago, our understanding of the interactions between the mask, sensor and algorithm has evolved significantly. Two key system-level improvements have taken place. The first is the improved computational efficiency made possible by jointly designing the optics and algorithms. The second is that the inherent multiplexing of lensless cameras provides an intimate connection to compressed sensing, leading to a design framework for lensless cameras capable of capturing more than simple 2D images.
With the ever-increasing pixel count of modern digital image sensors, mask and algorithms must be codesigned to allow for efficient computation. When imaging distant objects, each scene point will fill the entire mask. In this regime, most lensless cameras are characterized by a single PSF, leading to an efficient optical model based on 2D fast Fourier transform (FFT) convolutions. Some masks create PSFs that can be further reduced to two 1D FFT convolutions. These methods enable scalable algorithms that can provide image previews in near real time. However, even using these approximations, achieving high-quality results on pixel-dense sensors using optimization algorithms is still too computationally expensive to be practical in many applications.
The convergence speed of reconstruction algorithms depends greatly on the properties of the mask patterns. Designers have commonly developed merit functions for the mask pattern that are designed to improve convergence speed, but this does not jointly optimize optics and algorithm. End-to-end design has emerged as a method to address this. In this approach, a simulation of the optical system produces raw measurements using a set of ground-truth training images. The reconstruction algorithm then processes the raw data into candidate images. The error across the dataset is used to simultaneously refine the optical design and algorithm parameters. This framework allows designers to impose constraints on the system, such as the algorithm complexity, finding the optics and algorithm parameters that jointly maximize performance within those constraints.
Another important advance is using random masks to capture higher-dimensional images, thanks to the connection between lensless cameras and compressed sensing. Since the mid-2000s, compressed sensing has emerged as a framework for sampling signals with a large number of unknowns from a relatively small number of measurements. This requires that each point in the input space contribute to many output observations, a property called multiplexing. Provided this holds, certain high-resolution input signals can be reconstructed from a small number of observations by solving an optimization problem.
Applied to imaging, this means that an image can be recovered with space–bandwidth product significantly exceeding the number of sensor pixels. Lensless cameras are a natural fit for compressed sensing, because they multiplex each scene point into multiple sensor pixels, and the image is often recovered by solving a sparsity-constrained optimization problem. Multiple works applying compressed-sensing theory to lensless imagers have demonstrated this benefit.
 Using sparse recovery algorithms, pixels erased from data captured by a lensless camera are recovered from as few as 1.5% of the sensor pixels.
Using sparse recovery algorithms, pixels erased from data captured by a lensless camera are recovered from as few as 1.5% of the sensor pixels.
Pixel erasure, high-speed video and DIY masks
The most direct application of lensless cameras is imaging distant scenes in a thin camera. Numerous compact lensless cameras (or cameras combining thin-optics with algorithmic processing) have been proposed for photography, encoding image information using a variety of masks—including modified uniformly redundant arrays, Fresnel zone arrays, miniature diffractive optics, diffusers and regular or randomly spaced microlens arrays. Furthermore, lensless cameras have been jointly designed end-to-end to improve certain camera characteristics, such as learned diffractive optics for wide FoV, high dynamic range, or extended depth of field.
The distributed nature of their multiplexed measurements makes lensless systems robust to pixel erasure—in some cases, images can be recovered from as few as 1.5% of the sensor pixels. This concept has been utilized to compute snapshot multispectral images in a lensless camera using 64-channel narrowband color filter arrays on the sensor. Also, random phase masks have been used to encode sparse 3D information, light fields, high-speed video and multispectral information.
Rolling-shutter sensors expose each row of pixels over a unique time window. Used with lenses, rolling-shutter sensors distort fast-moving objects. However, the multiplexing of lensless cameras enables rolling shutter to be viewed as a benefit. As lensless cameras are robust to erasure, each sensor row can be viewed as a highly undersampled measurement of an instant during the exposure. In one recent work, for example, a random-mask lensless camera converted a conventional 30-fps CMOS sensor into a 4500-fps high-speed camera using compressed sensing.
Lensless cameras are also finding use in education, as researchers have demonstrated setups built with a range of “DIY” masks. In addition to the random-phase-mask example mentioned above, researchers have captured images using readily available materials such as plexiglass, random mirrors and two-sided tape. While the images are not of the highest quality, DIY masks offer a user-friendly, low-cost platform for introducing optics, inverse problems and computational imaging into classrooms and STEM outreach.
Macro- and micro-scale imaging
For scenes closer to the camera, the PSF can still be treated using 2D convolution, but the depth dependence of the PSF becomes an important factor. Typically, this requires calibrating the PSF from a set of depths across the desired imaging range. Consider, for example, a 3D scene close to the camera. With a lens, as the scene defocuses, high frequencies are destroyed and the image is soon unrecoverable. With a lensless camera, one can design the coding pattern so that each depth creates a unique, high-contrast pattern on the sensor. Depth map recovery, sparse 3D imaging, light field capture and digital refocusing have all been explored as benefits of this depth dependence.
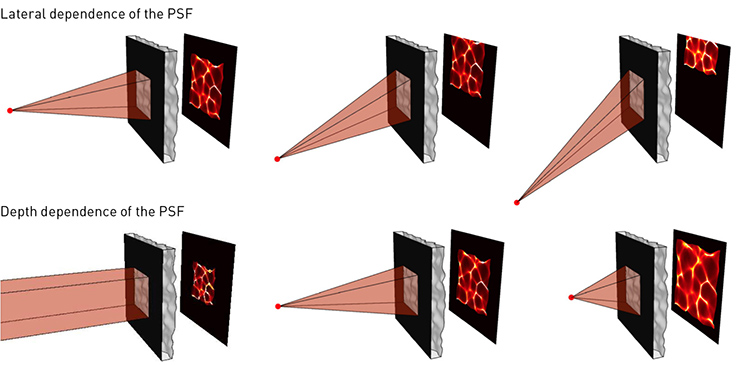 In the DiffuserCam setup, every point within the volumetric field-of-view projects a unique pseudorandom pattern of caustics on the sensor, enabling compressed sensing so that a sparse 3D scene can be recovered from a single 2D measurement. The patterns shift with lateral shifts of a point source in the scene and scale with depth. [N. Antipa et al. Optica, 5, 1 (2018)]
In the DiffuserCam setup, every point within the volumetric field-of-view projects a unique pseudorandom pattern of caustics on the sensor, enabling compressed sensing so that a sparse 3D scene can be recovered from a single 2D measurement. The patterns shift with lateral shifts of a point source in the scene and scale with depth. [N. Antipa et al. Optica, 5, 1 (2018)]
Toward lensless microscopy
To capture microscopic detail, objects must be brought within milimeters of the mask. This presents challenges for lensless cameras. In this geometry, light strikes the mask and sensor at extremely high angles. For a mask that weakly deflects rays, the measurement numerical aperture (NA) is determined by the maximum acceptance angle of the sensor. This is a somewhat strange property wherein the effective acceptance aperture of the system is determined by the angular behavior of the sensor, not a single well-defined stop surface. As a consequence, the system cannot be characterized using a single convolutional PSF because light from each field point passes through a unique region of the mask. Overcoming this requires more complex algorithms and calibration, which have been recently reported.
Additionally, to achieve high resolution, the mask must recombine light diffracted at high angles from the sample. This is difficult to achieve with single-surface mask designs, and often limits the effective resolution of mask-based microscopes to micron-scale and larger. Achieving diffraction-limited resolution on par with the NA set by the sensor is still an active area of research and development. Finally, illumination and high-quality fluorescence filters are difficult to integrate into a flat architecture. Despite these difficulties, in 2017, Rice University, USA, engineers reported imaging 3D fluorescent samples with their FlatScope at 1.6-μm resolution.
As these challenges are overcome, the upsides of lensless microscopes will be realized. The first such upside is the ability to scale the FoV without adding thickness to the device—opening the door to extremely thin, wide-FoV lensless microscopes. A lens-based telecentric microscope objective grows as the cube of the (linear) FoV. Lensless microscopes grow as the square, so they can achieve a very wide-FoV telecentric imaging system with much thinner form factor than with a conventional lens. With maximum FoV limited by the sensor, this design paradigm may be well positioned to keep pace with the ever-increasing bandwidth of commercial sensors.
In addition to an improved volume-to-FoV ratio, the inherent ability of these systems to encode depth and add spectral information sets the stage for wide-FoV 3D or hyperspectral microscopes. As the quality of masks and algorithms improve, these microscopes will become increasingly viable for sparse fluorescence imaging.
Originally inspired by extreme-wavelength imaging, lensless cameras have since emerged as an exciting new direction for imaging-system design across the electromagnetic spectrum.
Realizing these benefits comes at significant cost, however, with the effective NA of most lensless microscopes to date being far lower than commercial microscope objectives. Handling high-NA rays in lensless cameras will require more advanced fabrication and design techniques to reach competitive resolution and contrast. For sparse scenes this is viable—but for extremely dense bright field imaging, it’s unlikely that the multiplexing reduction in SNR can reasonably be overcome.
One exciting application area for lensless cameras is in functional neuroimaging, which has somewhat modest resolution requirements: neurons are tens of microns in diameter. Creating time-resolved wide-FoV cameras with single-neuron resolution may enable monitoring many neurons in vivo with compact sensing hardware. Overcoming limitations of one-photon neuroimaging, such as scattering, constitutes a major hurdle, but changes such as long-wavelength fluorophores may offer straightforward solutions once widely available.
 Compared with conventional microscopes, the weight of lensless microscope objectives scales as the square of the field of view, achieving a much thinner form factor and wide FoV. [Enlarge graphic]
Compared with conventional microscopes, the weight of lensless microscope objectives scales as the square of the field of view, achieving a much thinner form factor and wide FoV. [Enlarge graphic]
The (lensless) road ahead
While originally inspired by extreme-wavelength imaging, lensless cameras have since emerged as an exciting new direction for imaging-system design across the electromagnetic spectrum. They’re compact, can capture from photographic down to micron scales, and can encode extra scene information that would be destroyed in conventional imaging designs.
As optimization and machine-learning algorithms improve, the computational burden of these cameras will decrease, though it will likely always exceed what’s required for postprocessing conventional images. The reliance on accurate system calibration data presents another hurdle to wide-scale adoption of lensless cameras. Online self-calibration from passively captured data is an interesting research direction to address this limitation.
Designing and fabricating masks for microscopy remains an open challenge. New fabrication techniques like nanophotonics and 3D-printed gradient-index optics may offer avenues to push the resolution limits of lensless microscopes while also integrating illumination delivery and wavelength specificity.
This is an exciting time to work in the field of computational imaging for lensless cameras. We’re just scratching the surface of the application areas best suited to lensless imaging, and more investment is needed to fully explore the research area’s potential. Technological improvements in this space could impact a wide range of application domains.
Nick Antipa is an assistant professor of electrical and computer engineering at the University of California San Diego, USA.
References and Resources
-
J.G. Ables. “Fourier transform photography: A new method for X-ray astronomy,” Publ. Astron. Soc. Aust. 1, 172 (1968).
-
R.H. Dicke. “Scatter-hole cameras for X-rays and gamma rays,” Astrophys. J. 153, L101 (1968).
-
J.K. Adams et al. “Single-frame 3D fluorescence microscopy with ultraminiature lensless FlatScope,” Sci. Adv. 3, e1701548 (2017).
-
G. Kim and R. Menon. “Computational imaging enables a ‘see-through’ lensless camera,” Opt. Express 26, 22826 (2018).
-
N. Antipa et al. “DiffuserCam: Lensless single-exposure 3D imaging,” Optica 5, 1 (2018).
For an expanded list of references and resources, visit: www.osa-opn.org/link/lensless.
