Collage of structured light created in the laboratory with SLMs and DMDs. [University of the Witwatersrand]
Collage of structured light created in the laboratory with SLMs and DMDs. [University of the Witwatersrand]
Structured light refers to the tailoring or shaping of light in all its degrees of freedom—whether in time and frequency, to create ultrafast tailored time pulses; or, more commonly, in controlling light’s spatial degrees of freedom such as polarization, amplitude and phase. Although the term “structured light” was coined only about a decade ago, the notion of controlling light has a very long history. The first recorded account of tailoring light is the probably apocryphal tale, during the siege of Syracuse (circa 213–211 B.C.E.), of using multiple mirrors to shape the intensity of sunlight on Roman ships, setting them on fire—an example of multi-faceted incoherent beam shaping. Lenses and imaging systems likewise may be considered early forms of tailoring light.
Structured light refers to the tailoring or shaping of light in all its degrees of freedom.
It was the advent of the laser, however, that ushered in true control for structuring light. Better known as laser beam shaping (see “Laser beam shaping,” OPN, April 2003), the field took off in the late 1980s and early 1990s, driven by the interplay of optics and computing. Better optical techniques led to advances in lithography for smaller microelectronics, fueling faster computers; the improvement in computing power and lithographic techniques, in turn, allowed calculation and fabrication of new optical designs.
From DOEs to DMDs
This interplay saw the emergence of computer-generated holograms (CGHs), implemented as diffractive optical elements (DOEs). Previous Fourier “tricks” for advanced pattern recognition could now be generalized and implemented as high-performance, phase-only elements for arbitrary light control. Despite the potential, the uptake was mostly limited to shaping light intensity—for example, Gaussian-to-flat-top intensity converters for various industrial applications. The high fabrication cost of one-off elements, often running into tens of thousands of U.S. dollars, was a major hurdle. Meanwhile, free-form and aspheric technologies had not reached the versatility they enjoy today, so the cheaper option of refractive solutions was very limited.
The structured-light field advanced slowly until the development of commercial rewritable spatial light modulators (SLMs) for photonic applications. The foundations of today’s liquid-crystal-on-silicon (LCoS) SLMs were laid in the 1970s at Hughes Aircraft Corporation (following on the heels of the laser), but these only moved out of traditional projector markets and into photonic structured-light devices in the early to mid-2000s. This readily available, rewritable implementation technology fueled an explosion in structured-light research. Digital micromirror devices (DMDs)—which offer increased speed and reduced cost, at the expense of efficiency—promise a similar advance today.
All of these approaches and tools control the amplitude and dynamic phase of light. Another important component in any structured-light arsenal, however, is the exploitation of geometric phase, possible through liquid-crystal holograms and metasurfaces (see “Controlling light with geometric-phase holograms,” OPN, February 2016). Once again, computing power coupled with advances in fabrication technology is helping to reshape opportunities in photonics, affording the ability to easily tailor light’s polarization structure beyond spatially homogeneous states. That, combined with control of amplitude and dynamic phase, has allowed the easy creation of arbitrary forms of structured light—in many cases using commercial, off-the-shelf devices.
Amplitude, phase and polarization
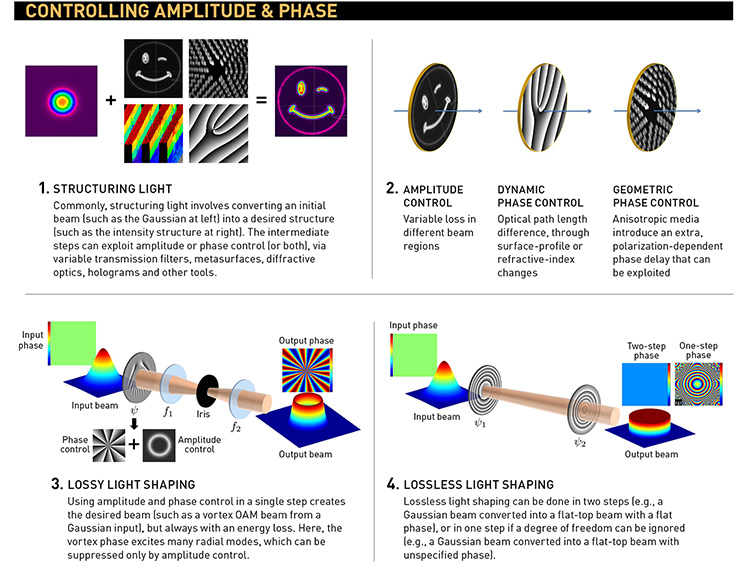
We would like a toolkit that makes it possible to take an initial optical field and reshape it to another in amplitude, phase and polarization. A variety of approaches exist to achieve amplitude and phase control of homogeneously polarized scalar beams (see “Controlling amplitude and phase,” above). Creating exotic polarization structures requires amplitude and phase control of each polarization vector in the optical field—of how the right-circularly and left-circularly polarized or linearly polarized components of the light appear. The sum of two components with differing spatial properties gives rise to vector states of light with spatially inhomogeneous polarization structures. For example, if the two circular polarization states have azimuthal phases of opposite helicity, the resulting beam will be a cylindrically symmetric vector structure: one example would be radially polarized light with linear polarization vectors that point radially everywhere.
 The laboratory creation of arbitrary structured light using geometric and dynamic phase control. The donut beams are scalar and vector OAM modes, the latter with spatially varying polarization structures. [University of the Witwatersrand]
The laboratory creation of arbitrary structured light using geometric and dynamic phase control. The donut beams are scalar and vector OAM modes, the latter with spatially varying polarization structures. [University of the Witwatersrand]
Since structured vector beams are just the sum of two structured scalar beams, the traditional toolkit for scalar beams can be applied separately and then added interferometrically. This exploits dynamic phase only. Geometric phase can also be exploited—via subwavelength structures on metasurfaces, or via large-scale structures in liquid crystals—to induce a phase change that differs for each polarization, so that the vector beam is created directly. Interestingly, in the early days of small-feature-size DOEs, vector effects were known but usually considered unwanted artifacts; today these effects offer full control of structured light.
Structured light from lasers
Structured light can also be created directly at the source, in so-called structured-light lasers. Researchers creating structured light from cavities in the early lasers used intracavity wires, stops and apertures to produce Hermite-Gaussian and Laguerre-Gaussian beams. Often intracavity approaches are used to “unstructure” light—for example, using a simple circular aperture to produce only a Gaussian mode and not many transverse modes, or using adaptive optics to remove phase structured from thermal aberrations. Gain control rather than loss control can also be used to create structured light from lasers—for instance, by dynamically shaping, with a DMD, the light field that pumps the laser.
Intracavity phase elements have been extensively used since the 1990s to produce exotic states of light from lasers. Such schemes work by defining a desired intensity and phase at the output of the laser and reverse-propagating it to the back mirror. If the mirror acts as a phase-conjugating element, then the desired beam will emerge again at the output. Since this process repeats after each round trip, the specified mode is an eigenmode of the cavity.
 Custom intracavity optical elements and geometries allows for structured light at the source. Here, an illustrative cavity with internal metasurfaces is shown to output twisted OAM modes. [University of the Witwatersrand]
Custom intracavity optical elements and geometries allows for structured light at the source. Here, an illustrative cavity with internal metasurfaces is shown to output twisted OAM modes. [University of the Witwatersrand]
A structured-light form of particular popular interest is light carrying orbital angular momentum (OAM)—“donut”-looking beams characterized by an azimuthally twisted phase profile and a central intensity null (see “Light served with a twist,” OPN, June 2017). Creating OAM modes directly from a laser is not an easy task, as nature cannot tell the difference between a clockwise and anticlockwise twisted mode: they have the same propagation dynamics, the same beam sizes, the same wavefront curvature and so on, making them hard to distinguish in a laser. Paradoxically, creating such beautifully symmetric modes usually requires some form of symmetry breaking. One such approach is to use geometric phase, via exotically structured matter, to produce novel states of structured light.
A menu of structured light
The toolkit outlined above has enabled creation of many forms of structured light. These include well-known eigenmodes of free-space in the form of Hermite-Gaussian (HG), Laguerre-Gaussian (LG) and more general Ince-Gaussian (IG) beams, as well as eigenmodes of many optical-fiber systems, including lineraly polarized (LP) and cylindrical vector vortex (CVV) modes.
Considering only specific aspects of the light field, rather than its totality, lets one engineer light that bends the rules of physics. One example is “nondiffracting” Bessel beams, which appear to propagate without spreading—but only if the central region of the beam is considered. Another is the famous Airy beam, which seems to accelerate transversely and propagate on a curved trajectory—but only if the main lobe alone is considered; the entire beam follows a straight-line path at a constant speed.
General forms of structured light have since been shown, including radial and angular accelerating optical beams, photonic hooks, caustic beams, elegant LG and HG beams, and exotic polarization singularity structures that include so-called lemon, star, monstar, spider, web and flower states. OAM states of light show twisted helical phase structures, like a spiral staircase; the twist can be clockwise or anticlockwise, and twisted once, twice, three times or more per wavelength—resulting in a phase singularity at the beam center and a zero-intensity region that increases with the amount of twist.
The creation of these 2D transverse states can be generalized to arbitrary 3D structured light in some region of space, usually about some focal point. Examples of this include the creation of polarization Mobius-strip beams, knotted singularities in phase and polarization, Talbot array beams and fractal states of light. Sometimes it is beneficial to keep one dimension small, as is the case of light sheets for microscopy, or to make the 2D structure change during propagation for 3D light.
Recently 2D light has been modulated at many planes by multiple 2D phase modifications, evolving simple structured light into more exotic multimodal forms, useful for both creation and detection in the context of optical communication, and even as high-dimensional quantum gates. Still another emerging field is the 4D control of light—spatial and temporal control—which remains largely unexplored.
The notion of quantum states of structured light offers a particularly intriguing angle on detection—quantum detection plays a role analogous to classical creation.
Detecting structured light
Having created structured light, we also want to detect it. In most cases, light’s reciprocity allows the detection step to be the creation step run backwards. Unraveling the phase, amplitude and polarization recovers the initial beam—often a Gaussian. A simple single-pixel detector or coupling to a single-mode fiber allows quantitative analysis of the field by modal decomposition. These approaches—essentially nothing more than the match-filter technology from early optical pattern recognition—can be made more efficient by sorting various modes deterministically using two-step lossless conformal mapping. Such mode sorters have been developed and applied to LG, HG and Bessel beams (see “Unraveling Bessel beams,” OPN, June 2013).
 A single UV photon creates two spatially entangled bi-photons by SPDC in a nonlinear crystal, shown here as entangled twisted light modes. [University of the Witwatersrand]
A single UV photon creates two spatially entangled bi-photons by SPDC in a nonlinear crystal, shown here as entangled twisted light modes. [University of the Witwatersrand]
The notion of quantum states of structured light offers a particularly intriguing angle on detection—quantum detection plays a role analogous to classical creation. In a vanilla version of a quantum experiment with structured light, a Gaussian pump excites a spontaneous parametric down-conversion (SPDC) process in a nonlinear crystal to produce two photons entangled in their spatial mode. But the state is not defined until it is measured: the entanglement could be expressed in any spatial mode, so one cannot speak of the two photons as “being” HG, LG or Bessel modes. The post-selection of one pattern versus another collapses the state into the one that’s measured.
Because many spatial mode sets are orthogonal and complete, they form a natural way to express the entanglement. Simply put, this is quantum mechanics with patterns of light, and it works because the patterns can be unique. The hope is to exploit the infinite number of patterns to access infinitely large Hilbert spaces—both for asking fundamental questions of quantum mechanics, and for exploiting entanglement as a resource.
Light tailored to fit
Given the versatility in control of structured light fields, it is not surprising that they have found many applications across multiple disciplines.
Structured light: Some applications
 Optical trapping/tweezing: Polarization nano-tomography of tightly focused light landscapes by self-assembled monolayers. [Courtesy of Eileen Otte, University of Münster]
Optical trapping/tweezing: Polarization nano-tomography of tightly focused light landscapes by self-assembled monolayers. [Courtesy of Eileen Otte, University of Münster]
 Materials processing: Cutting of ultrathin (<50 µm) and thick (>10 mm) glasses using ultrashort pulsed lasers and non-diffracting beams. The self-reconstructing beam enables high-quality separation of transparent materials by controlling crack orientation during the formation of a breaking layer. [Courtesy of Daniel Flamm, Trumpf]
Materials processing: Cutting of ultrathin (<50 µm) and thick (>10 mm) glasses using ultrashort pulsed lasers and non-diffracting beams. The self-reconstructing beam enables high-quality separation of transparent materials by controlling crack orientation during the formation of a breaking layer. [Courtesy of Daniel Flamm, Trumpf]
 Communications: The spatial degree of freedom holds tremendous promise for increasing present optical bandwidth: new information channels could be created by encoded information into the patterns of light. [University of the Witwatersrand]
Communications: The spatial degree of freedom holds tremendous promise for increasing present optical bandwidth: new information channels could be created by encoded information into the patterns of light. [University of the Witwatersrand]
Optical trapping and tweezing. Because trapping relies on the gradient force—proportional to the gradient of the intensity—tailoring light opens new possibilities. Beyond the ubiquitous Gaussian mode, traps have been designed using OAM modes to form optical “spanners” that rotate matter at ultrafast speeds; Airy beams for optically mediated particle clearing; Bessel beams to trap particles at multiple planes, optically sort blood cells and form optical conveyer belts as counter-propagating light fields—to name but a few. Structured light has been instrumental in controlling matter and flow in microfluidic systems, and the interaction of structured light and structured matter is essential for control at the nanoscale through near-field effects.
Super-resolution microscopy. Stimulated-emission depletion (STED) microscopy, one of the technologies recognized by the 2014 Nobel Prize in chemistry, is enabled by use of two forms of pulsed structured light. A first (usually Gaussian) pulse excites fluorophores inside the illuminated region, and a second (usually hollow) pulse returns the fluorophores within the ring-shaped area to the ground state via stimulated emission. Thus only molecules within the center of the STED beam will fluoresce, allowing the point-spread function to narrow and increasing resolution beyond the diffraction limit. STED microscopy has achieved up to 20 nm lateral resolution and up to 40 nm axial resolution.
It’s hoped that structured light can continue to address challenges in microscopy—poor contrast in unstained biological samples, limited spatio-temporal resolution, the difficulty of looking deep into light-scattering samples—in both the illumination and detection stages. Here the form of the light is paramount: light sheets for selective plane imaging; iterative beam shaping to optimally structure light to see deeper into scattering tissue; LG beams as the hollow beam for STED.
Manufacturing. Laser-enabled manufacturing has long used structured light to increase processing speed and quality and to optimize cost and efficiency. Tailoring the intensity profile has led to efficient drilling—for example, VIA drilling for microelectronics with flat-top beams—while polarization control has been essential for cutting along arbitrary geometries. For metal cutting with a large ratio of sheet thickness to width, radially polarized light offers a cutting efficiency twice as large as with linearly polarized beams.
Vector beams have also come to the fore because of their efficacy in removing waste material from the interaction zone, and the ability to focus tightly with strong longitudinal field components. In fact, tuning transverse and longitudinal field components enables arbitrary shaping of the focal spot, facilitating flat-top intensity profiles at the focus without traditional beam shapers. Nondiffracting beams have recently improved the cutting of thin and thick glasses and etching of 2D contours.
Communications bandwidth and security. The idea of using spatial modes of light as a new degree of freedom in optical communications dates back to the early 1980s but has gained traction in the past decade, based on both increasing need and a readily available toolkit. Ideally, each pattern would act as a new channel carrying the maximum information capacity possible with present technologies, with N patterns translating to an N-fold bandwidth gain. In reality, coupling between spatial modes in optical fiber and turbulent free-space limits the channel capacity, while digital signal processing correction becomes prohibitive for large, multi-channel systems.
Nevertheless, faster communication with structured light has exceeded terabit-per-second speeds, with ever-increasing distances demonstrated using custom-designed fiber. After a seminal demonstration down the corridors of the University of Glasgow, U.K., around 15 years ago, OAM has been the mode of choice, but studies have shown the potential benefit of other modes—for example, Bessel beams for self-healing links, HG beams for resilience to tip and tilt, and combinations of mode types that experience channels differently to leverage diversity, the other side of the mode-division-multiplexing coin.
Meanwhile, structured light at the quantum level could hold the key to improved data security. Many patterns offer access to a high-dimensional quantum state, known to allow higher information capacity per photon and a higher tolerance level to noise—both vital for quantum key distribution (QKD). The first QKD with structured light was performed with OAM and its mutually unbiased bases, followed by QKD and entanglement preservation through obstacles with Bessel states, and long-range free-space (up to around 300 m) and fiber (up to around 1 km) quantum links with hybrid entangled modes in polarization and OAM. While the quantum toolkit for structured light is still far behind that for polarization, the potential benefits are driving rapid progress in the field.
It has never been easier to get started with structuring of light—and, pertinently, everyone is working with some form
of structured light, even if not by design.
Open challenges and opportunities
Various national photonics strategies have labeled this the century of the photon, with the promise of photonics replacing much of electronics. Yet despite centuries of effort, we do not have the same control in photonic systems as we have in electronic systems. The toolkit for controlling structured light, while substantially enriched in recent years, is still mostly empty: we have few options for compact sources of structured light, few easily available solutions that are not custom-made, and few that work at higher power levels and/or fast switching rates. At present, to deploy a structured-light solution, the user must be a structured-light expert. That’s akin to asking all microscope users to first design their own objectives!
Yet it has never been easier to get started with structuring of light—and, pertinently, everyone is working with some form of structured light, even if not by design. Rather than use the light from your laser as it comes, why not tailor it for your particular application? This is the opportunity: structured light, tailored for purpose.
The author thanks Michael De Oliviera, Isaac Nape, Jonathan Pinnell and Bereneice Sephton for assistance with the graphics.
OSA Fellow Andrew Forbes is with the School of Physics at the University of the Witwatersrand, Johannesburg, South Africa.
References and Resources
-
H. Rubinsztein-Dunlop et. al. “Roadmap on structured light,” J. Opt. 19, 013001 (2017).
-
M. Erhard et al. “Twisted photons: New quantum perspectives in high dimensions,” Light Sci. Appl. 7, 17146 (2018).
-
E. Otte et al. “Polarization singularity explosions in tailored light fields,” Laser Photon. Rev. 12, 1700200 (2018).
-
C. Rosales-Guzman et al. “A review of complex vector light fields and their applications,” J. Opt. 20, 123001 (2018).
-
A. Forbes. “Structured light from lasers,” Laser Photon. Rev. 13, 1900140 (2019).
-
A. Forbes and I. Nape. “Quantum mechanics with patterns of light: Progress in high dimensional and multidimensional entanglement with structured light,” AVS Quantum Sci. 1, 011701 (2019).
-
G. Lazarev et. al. “Beyond the display: Phase-only liquid crystal on silicon devices and their applications in photonics,” Opt. Express 27, 16206 (2019).
-
Y. Shen et al. "Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities," Light Sci. Appl. 8, 90 (2019).