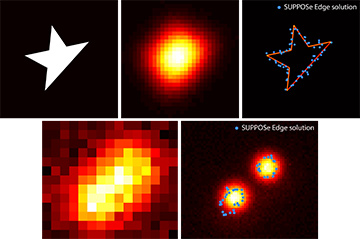
 Top: An artificial image of a truncated star shape (left) is convolved with the microscope PSF, and noise is added (center). The blue dots (right) show the SUPPOSe algorithm’s reconstruction of the edge, superimposed on the ground-truth shape. Bottom: Image of fluorescent beads with a 10x objective (left) and edge reconstruction, overlapped with a 40x objective image. [see videos]
Top: An artificial image of a truncated star shape (left) is convolved with the microscope PSF, and noise is added (center). The blue dots (right) show the SUPPOSe algorithm’s reconstruction of the edge, superimposed on the ground-truth shape. Bottom: Image of fluorescent beads with a 10x objective (left) and edge reconstruction, overlapped with a 40x objective image. [see videos]
Edge detection in images is a key problem in quantitative cell biology, nanophotonics and other areas. But while many edge-detection algorithms have been developed, all suffer from serious limitations in precision—indeed, one study on quantifying cell migration showed that changing the method of edge detection or one of its parameters can cause edge estimations to vary by up to 25%.1 This year, we presented a computational method for super-resolution edge detection in single standard images that opens the possibility of detecting shapes of objects with features much smaller than the microscope’s point spread function (PSF).2
Our work rests on a deconvolution algorithm we recently presented, SUPerposition of POint Sources (SUPPOSe),3,4 which approximates the object to be reconstructed by a superposition of virtual point sources of equal intensities. In this algorithm, the random initial positions of the point sources evolve toward a solution that resembles the ground truth, with a precision much smaller than the PSF width (see video). Whereas other deconvolution techniques lose resolution because they must impose regularization terms to overcome the fact that the mathematical problem is ill posed, SUPPOSe does not, because the fact that the source intensity is positive by definition is included in its formulation.
One limitation of the SUPPOSe algorithm is that the source has to be somewhat sparse3 and hence it cannot be applied to dense objects. In our work published this year, we found that by fitting the edge with a discrete number of point sources, and fitting the gradient of the image, the gradient of the object can be found using a modified SUPPOSe method.2
We view this as a major contribution to the deconvolution of microscopy images, as it enables the shape of objects smaller than the microscope’s PSF to be recovered, as shown in the figure. Our work thus far2–4 has used fluorescence microscopy images. However, the only requirement of the formalism we have presented is a lack of spatial coherence (that is, the different points must add in intensity). Hence, the technique can be extended to any noncoherent microscopy technique for which other super-resolution methods such as STORM, STED and PALM do not apply.
Researchers
Guillermo D. Brinatti Vazquez, Axel M. Lacapmesure, Micaela Toscani, Sandra Martínez and Oscar E. Martínez, Universidad de Buenos Aires, Argentina
References
1. K.K. Treloar and M.J. Simpson. PLoS One 8, e67389 (2013).
2. G.D. Brinatti Vazquez et al. Opt. Express 28, 25319 (2020).
3. S. Martínez et al. J. Microsc. 275, 51 (2019).
4. A.M. Lacapmesure et al. Proc. Gen. Evol. Comp. Conf. 2020, 271 (July 2020).
