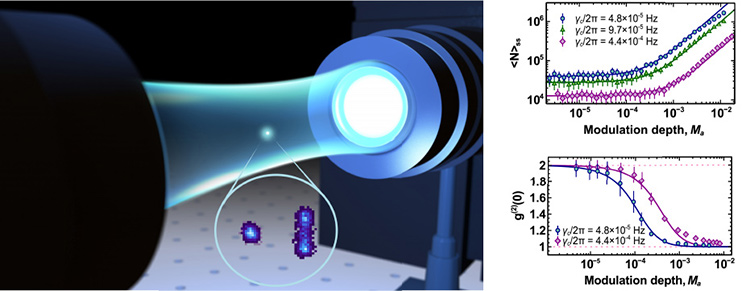
 Left: Artist’s rendering of a silica nanosphere levitating in an optical tweezer. The inset shows a density map of particle center-of-mass motion revealing (left) Brownian motion below threshold and (right) coherent oscillation above threshold. Top right: Threshold behavior of the steady-state phonon number as a function of linear gain (given by the optical modulation depth, Ma) for various nonlinear cooling strengths, gx. Bottom right: Second-order phonon autocorrelation function at zero-time delay, showing the transition from thermal to nearly Poissonian phonon statistics.
Left: Artist’s rendering of a silica nanosphere levitating in an optical tweezer. The inset shows a density map of particle center-of-mass motion revealing (left) Brownian motion below threshold and (right) coherent oscillation above threshold. Top right: Threshold behavior of the steady-state phonon number as a function of linear gain (given by the optical modulation depth, Ma) for various nonlinear cooling strengths, gx. Bottom right: Second-order phonon autocorrelation function at zero-time delay, showing the transition from thermal to nearly Poissonian phonon statistics.
Lasers—devices that amplify light based on stimulated emission of optical photons—have enabled wide-ranging technological and scientific advances since their first demonstration in 1960.1 Theoretical and experimental advances have since extended the essential physics behind laser operation to the regime of mechanical vibrations, bringing about the concept of a “phonon laser,” which amplifies mechanical vibrations through the analogous process of stimulated emission of mechanical phonons. Such devices could find application in high-precision sensing, mechanical-state engineering and information processing.
In recent work, we merged the phonon laser with another transformational technology: the optical tweezer.2 This technique, which brought dramatic new capabilities for manipulating matter on the micro and nano scales, gained the 2018 Nobel Prize in Physics for its principal inventor, Arthur Ashkin.3
In our work, a levitated nanosphere in an optical tweezer forms a mechanical resonator with multiple degrees of freedom; our study focused on the center-of-mass modes. Using optical feedback based on picometer-scale measurements of the nanosphere’s center of mass to modulate the intensity of light in the tweezer, we demonstrated and modeled the essential physics of stimulated emission of center-of-mass phonons into the vibrational mode, resulting in an optical-tweezer phonon laser.
The applied feedback signals are derived from a parametric cooling loop, which reduces the number of center-of-mass phonons and provides the necessary nonlinearity, and an anti–damping signal, which gives rise to linear amplification analogous to a laser gain medium. The combined effect of both feedback signals leads to threshold behavior in the steady-state phonon number and a transition from thermal to nearly Poissonian phonon statistics.
We expect this demonstration to have broad applicability in levitated-optomechanics experiments4 as a source of coherent phonons at the mesoscale, providing new approaches to precision metrology as well as a pathway toward the generation of nonclassical optomechanical (e.g., levitated Schrödinger cat) states.
The authors acknowledge support from the Office of Naval Research under award Nos. N00014-17-1-2285, N00014-18-1-2370, N00014-14-1-0803 and N00014-17-1-2291.
Researchers
Robert M. Pettit, Danika R. Luntz-Martin, Justin T. Schultz and A. Nick Vamivakas, University of Rochester, Rochester, N.Y., USA
W. Ge and P. Kumar, Rochester Institute of Technology, Rochester, N.Y., USA
M. Bhattacharya, Rochester Institute of Technology and University of Rochester
Levi P. Neukirch, Los Alamos National Laboratory, Los Alamos, N.M., USA
References
1. T.H. Maiman. Nature 187, 493 (1960).
2. R.M. Pettit et al. Nat. Photon. 13, 402 (2019).
3. A. Ashkin et al. Opt. Lett. 11, 288 (1986).
4. A.N. Vamivakas et al. Opt. Photon. News, 42 (July/August 2016).
