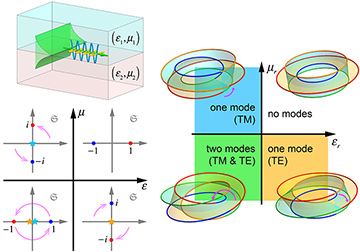
 Top left: Schematic of surface TM/TE electromagnetic waves at the interface between two optical media. Bottom left: Evolution of the complex spectrum of the non-Hermitian helicity operator S between media with different signs of the permittivity (ε) and permeability (μ). Right: Topological phase diagram of the TM and TE surface modes at interfaces with different relative parameters εr = ε2/ε1 and μr = μ2/μ1, which is explained by the bulk-boundary correspondence and Z4 (double-Möbius) winding of the helicity spectrum. [Enlarge figure]
Top left: Schematic of surface TM/TE electromagnetic waves at the interface between two optical media. Bottom left: Evolution of the complex spectrum of the non-Hermitian helicity operator S between media with different signs of the permittivity (ε) and permeability (μ). Right: Topological phase diagram of the TM and TE surface modes at interfaces with different relative parameters εr = ε2/ε1 and μr = μ2/μ1, which is explained by the bulk-boundary correspondence and Z4 (double-Möbius) winding of the helicity spectrum. [Enlarge figure]
Surface electromagnetic waves at boundaries between optical media play a crucial role in plasmonics and metamaterials. Their study started with the discovery of surface plasmon polaritons at metal-dielectric interfaces in the 1950s and was reinvigorated by the development of negative-index metamaterials.1 Today there is enormous interest in topological surface waves in quantum and classical wave systems. Differences in the topological properties of the two media make such waves robust against certain classes of perturbations, enabling systematic design of reflection-free waveguides.2
Originally, condensed-matter physicists developed theories of topological surface modes based on Hermitian wave Hamiltonians hosting band gaps. Recently, the ability to include gain and loss in photonics, described by non-Hermitian Hamiltonians, has inspired a new branch of topological physics applicable to active devices such as lasers.3 Yet both existing theories, based on gapped wave Hamiltonians, ultimately have a limited applicability to microstructured optical media supporting photonic band gaps, such as photonic crystals.
In recent work, we have shown that these areas of research are strongly and fundamentally linked with each other on the level of the most basic form of Maxwell’s equations describing isotropic, lossless, homogeneous optical media.4 We found that the necessary conditions for the appearance of transverse magnetic/transverse electric (TM/TE) surface electromagnetic waves—the sign change of the permittivity/permeability across the interface—originate from a topological bulk–boundary correspondence, which explains their robustness with respect to deformations of the interface, perturbations of material parameters, and dispersion.
This topological origin is special because it stems from the photon helicity operator (rather than the wave Hamiltonian), which is non-Hermitian even in lossless media. Discrete rotations of the complex helicity spectrum between media with different signs of the permittivity/permeability determine the Z4 (or double-Z2) group topology, which produces the fundamental phase diagram of surface electromagnetic modes. Importantly, the non-Hermitian origin affects properties of the surface modes, which generally have complex frequencies and propagation constants.
Thus surface electromagnetic modes,1 including surface plasmon polaritons, can be regarded as topological surface modes discovered half a century before topological quantum states.2 Our approach can be extended to surface waves in acoustics, explaining the appearance of “acoustic surface plasmon polaritons” at interfaces where the mass density changes its sign.5
Researchers
K.Y. Bliokh, RIKEN Cluster for Pioneering Research, Saitama, Japan, and The Australian National University, Canberra, Australia
D. Leykam, Institute for Basic Science, Daejeon, Republic of Korea
M. Lein, Tohoku University, Sendai, Japan
F. Nori, RIKEN Cluster for Pioneering Research, Saitama, Japan, and University of Michigan, Ann Arbor, Mich., USA
References
1. A. Alù et al. IEEE Antennas Propag. Mag. 49, 23 (2007).
2. T. Ozawa et al. Rev. Mod. Phys. 91, 015006 (2019).
3. R. El-Ganainy et al. Nat. Phys. 14, 11 (2018).
4. K.Y. Bliokh et al. Nat. Commun. 10, 580 (2019).
5. K.Y. Bliokh and F. Nori. Phys. Rev. Lett. 123, 054301 (2019).
