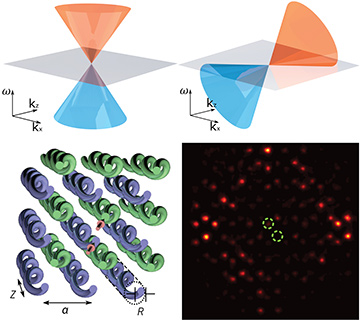
Top: Weyl dispersion relation [frequency ω versus momentum (kx,ky,kz) for constant ky = 0] for (left) type-I and (right) type-II Weyl points. The gray plane is an isofrequency cut. Bottom left: Schematic of the waveguide array exhibiting a type-II Weyl point, composed of two interpenetrating square lattices of helical waveguides. Bottom right: Intensity plots at the output facet showing conical diffraction at the Weyl point. The light rapidly diffracts away from the waveguides into which light is injected, indicated by green dashed circles.
A Weyl fermion is a hypothetical massless fundamental particle, predicted by Hermann Weyl in 1929 but so far never observed in nature.1 This particle has energy that is linearly proportional to its momentum—that is, it behaves like a massless relativistic spin-½ particle in 3-D. This “massless dispersion relation” can be mimicked in 3-D crystals exhibiting band degeneracies called Weyl points.
Mathematically, Weyl points are equivalent to quantized magnetic monopoles. That imbues them with “topological protection” against imperfections and disorder, and gives rise to exotic surface states known as Fermi arcs—highly promising features for future high-speed electronic and photonic devices. In 2015, the first observations of Weyl points were simultaneously reported in a condensed-matter system2 and a microwave photonic crystal, 3 and Physics World included those findings among the top 10 physics discoveries for the year.
The original microwave realization of Weyl points was based on an intricate double-gyroid photonic crystal machined out of high-refractive-index materials. Such a design is extremely challenging to extend to the critical optical wavelength regime, however, due to limitations in fabrication methods at the micron scale and the lack of sufficiently high-index materials. In 2017, we succeeded, using a waveguide array–based design, in observing Weyl points at optical frequencies.4
In our work, we used a femtosecond laser5 to inscribe a 3-D waveguide structure into borosilicate glass. Despite the simple staggered-helix design and low refractive-index contrast, we predicted that the structure could exhibit an anisotropic (type-II) Weyl-point at optical wavelengths. Using a combination of modeling and experiment, we demonstrated two key signatures for the presence of Weyl points. First, we showed that light propagating precisely at the Weyl-point wavelength undergoes conical diffraction. Second, we showed that Fermi-arc surface states emerge above (but not below) the Weyl-point wavelength.
We believe that this optical Weyl-point platform can be used in the future to probe Weyl-point photonic physics in new regimes, including those in which nonlinearity and quantum effects arise.
Researchers
Jiho Noh and Mikael C. Rechtsman, The Pennsylvania State University, University Park, Penn., USA
Sheng Huang and Kevin P. Chen, University of Pittsburgh, Penn., USA
Daniel Leykam and Y. D. Chong, Nanyang Technological University, Singapore
References
1. H. Weyl. Z. Für Phys. 56, 330 (1929).
2. S.-Y. Xu et al. Science 349, 613 (2015).
3. L. Lu et al. Science 349, 622 (2015).
4. J. Noh et al. Nat. Phys. 13, 611 (2017).
5. A. Szameit and S. Nolte. J. Phys. B 43, 163001 (2010).
Note: The authors wish to acknowledge the following funding agencies. M.C.R. acknowledges the National Science Foundation under award number ECCS-1509546, the Penn State MRSEC, Center for Nanoscale Science, under award number NSF DMR-1420620, and the Alfred P. Sloan Foundation under fellowship number FG-2016-6418. K.P.C. acknowledges the National Science Foundation under award numbers ECCS-1509199 and DMS-1620218. D.L. and C.Y.D. acknowledge support by the Singapore National Research Foundation under grant No. NRFF2012-02, by the Singapore MOE Academic Research Fund Tier 2 Grant No. MOE2015-T2-2-008, and by the Singapore MOE Academic Research Fund Tier 3 grant MOE2011-T3-1-005.