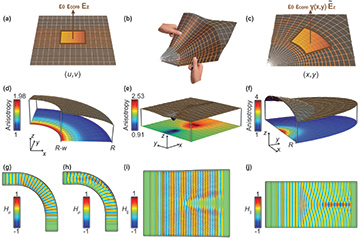
 Coordinate-based design of dielectric waveguides (a to c) results in all-dielectric metamaterial cores of varying thickness that can bend (d), split (e) and focus (f) light. Anisotropy of the metamaterial core (colored plane) and the thickness variation (grey floating surface, representing the upper interface) successfully manipulate in-plane magnetic fields (g), (i) and (j). Without a thickness variation the beam bender does not perform as desired (h).
Coordinate-based design of dielectric waveguides (a to c) results in all-dielectric metamaterial cores of varying thickness that can bend (d), split (e) and focus (f) light. Anisotropy of the metamaterial core (colored plane) and the thickness variation (grey floating surface, representing the upper interface) successfully manipulate in-plane magnetic fields (g), (i) and (j). Without a thickness variation the beam bender does not perform as desired (h).
Optical metamaterials provide exciting prospects for tackling fundamental challenges in photonics.1 A major opportunity lies in precisely manipulating light in integrated optics systems such as in sensors and optical circuitry. Such applications currently use photonic-band-gap materials or plasmon polaritons on material interfaces to benefit from strong light confinement. Unfortunately, plasmon-based waveguides suffer from a trade-off between the light’s confinement and its propagation range.2 For long-range applications, researchers have increasingly relied on the diverse optical properties of all-dielectric metamaterials.3
Can one design an optical device in a waveguide geometry using these dielectric metamaterials? This year, we proposed a design tool for dielectric metamaterial waveguides based on coordinate transformations.4 Our approach allows us to transform light trajectories along a two-dimensional plane until they conform to the needs of the application in question.
As other research has shown, specific metamaterials may implement such coordinate-based light trajectories, leading to impressive optical designs such as invisibility cloaks.5 For integrated optics systems where light travels along the surface of an optical chip, however, the exact reproduction of Maxwell’s equations leads to impractical and bulky designs, with metamaterials packed both inside and outside of the waveguide.
In our work, we have developed a specific materialization of the coordinate-transformed waveguide that uses artificial metamaterials only inside the waveguide core. To achieve this, we reproduce not the entire set of Maxwell’s equations, but only those that characterize a guided mode. This provides a waveguide design consisting of a uniaxial metamaterial core, complemented with a specific thickness variation of the core’s boundaries. The higher the coordinate deformation, the more the core’s anisotropy and thickness increase to steer the light in the desired direction, while preserving the continuity of its transverse profile at the waveguide’s interfaces (see figure).
Our designs of a beam bender, beam splitter and conformal lens efficiently reproduce the desired light flows along the waveguide plane. Our work, we believe, paves the way for long-range, low-loss manipulation of confined light with multifunctional coordinate-based waveguides.
Researchers
Sophie Viaene, Vincent Ginis and Jan Danckaert, Vrije Universiteit Brussel, Belgium
Philippe Tassin, Chalmers University of Technology, Gothenburg, Sweden
References
1. J.B. Pendry. Nat. Mater. 5, 599 (2006).
2. B. Dastmalchi et al. Adv. Opt. Mater. 4, 177 (2016).
3. S. Jahani and Z. Jacob. Nature Nanotech. 11, 23 (2016).
4. S. Viaene et al. Phys. Rev. B 93, 085429 (2016).
5. D. Schurig, et al. Science 314, 977 (2006).
