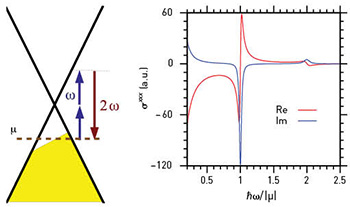
(Left) Resonant transitions for second harmonic generation, and (right) its effective nonlinear conductivity as a function of the photon energy ℏω divided by the chemical potential μ.
Optical nonlinearities play a central role in the operation of a wide variety of integrated photonic devices, such as on-chip broadband light sources, electro-optic modulators, optical switches and optical transistors. The availability of mature CMOS mass-manufacturing technology, developed for silicon electronics, exerts an inexorable pull toward the implementation of these photonic devices on silicon platforms. Yet while silicon has a relatively high third-order optical nonlinearity, its second-order optical nonlinearity vanishes because of its centrosymmetric crystal structure. This has hindered the realization of all-silicon nonlinear optical integrated circuits.
With its strong affinity for interacting with photons and its unique electronic properties, graphene is an exciting new candidate for providing nonlinear optical functionalities in on-chip optical devices. In addition, the integration onto silicon chips of this revolutionary material, consisting of a one-atom thick layer of carbon, is rapidly maturing. After pioneering nonlinear optical experiments,1 various optical experiments on graphene have demonstrated optical nonlinearities orders of magnitude higher than those of other nonlinear materials. However, a systematic approach to understanding graphene’s optical nonlinearities has been lacking. This is essential for identifying the most suitable material parameters—particularly the graphene doping level—for integrated graphene-on-silicon-based optical devices.2
By applying a standard perturbative theory at zero temperature, accounting for both the intraband and interband motion of electrons around the Dirac points, we have obtained analytic expressions for graphene’s third-order nonlinearities, providing new physical insight into their behavior over a wide range of chemical potentials and photon energies.3
We have also found that, despite its inversion symmetry, graphene’s unique electronic properties enable the generation of strong second-order nonlinear processes, such as second-harmonic generation (SHG), if a DC charge current is applied to break the symmetry.4,5 The effective second-order susceptibility reaches its maximum value when the fundamental photon energy matches the chemical potential. For a high-quality graphene sample with the appropriate chemical potential, the SHG efficiency can become several orders of magnitude higher than that of usual materials, at DC current densities that are feasible for device applications.
Taking into account the easy tunability of its chemical potential via either an external gate voltage or chemical doping, we thus find that graphene offers not only a strong optical nonlinearity, but a nonlinearity that is controllable. This makes graphene a most promising material for integrated nonlinear optics.
Researchers
J.L. Cheng, B-PHOT, Vrije Universiteit Brussel, Belgium, and Institute for Optical Sciences, University of Toronto, Canada
N. Vermeulen, B-PHOT, Vrije Universiteit Brussel
J.E. Sipe, Institute for Optical Sciences, University of Toronto
References
1. E. Hendry et al. Phys. Rev. Lett. 105, 097401 (2010).
2. N. Horiuchi. Nat. Photon. 8, 585 (2014).
3. J.L. Cheng et al. New J. Phys. 16, 053014 (2014).
4. A.Y. Bykov et al. Phys. Rev. B 85, 121413 (2012).
5. J.L. Cheng et al. Opt. Express 22, 015868 (2014).