 Resonant excitation of electric and magnetic Mie modes in dielectric nanoparticles of different sizes can allow unidirectional scattering of light from a broadband source. [Illustration by Phil Saunders]
Resonant excitation of electric and magnetic Mie modes in dielectric nanoparticles of different sizes can allow unidirectional scattering of light from a broadband source. [Illustration by Phil Saunders]
In nanophotonics, subwavelength localization of light is usually associated with plasmonics, the collective excitation of electrons and electromagnetic waves at metallic surfaces. Recent developments in the physics of high-index dielectric nanoparticles, however, suggest an alternative mechanism of light localization: electric and magnetic dipole and higher-order multipole Mie resonances.
These resonances can generate a strong magnetic response that can be leveraged in designing metasurfaces with unidirectional scattering, as well as efficient metadevices. Indeed, as the power of this approach becomes increasingly apparent, high-index nanomaterials could complement, or even substitute for, plasmonic materials in a range of devices—and could spur a new era in nonlinear nanophotonics.
From Mie scattering to optical magnetism
The physics of light scattering by subwavelength particles commonly involves Rayleigh scattering or surface-plasmon interactions, such as those that drive the varying colors of colloidal solutions of gold nanoparticles. These interactions depend only on material properties, not on particle shape. Mie-type resonances (also called morphology-dependent resonances), by contrast, hinge on both the size and the geometry of the particle in question. And an increasing recent understanding of optical Mie resonances of high-refractive-index dielectric nanoparticles has made it possible to facilitate light manipulation below the free-space diffraction limit.
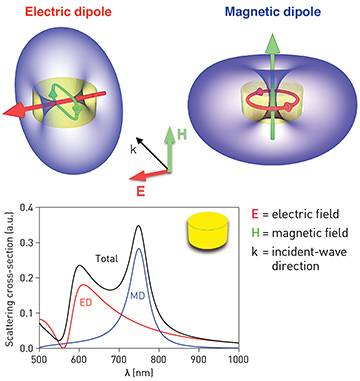 A silicon nanodisk, illuminated by a plane wave, produces both an electric dipole (ED) and magnetic dipole (MD) contribution to the total radiation pattern. (The ED contribution shows the asymmetric pattern of a Fano resonance.) [A. Miroshnichenko]
A silicon nanodisk, illuminated by a plane wave, produces both an electric dipole (ED) and magnetic dipole (MD) contribution to the total radiation pattern. (The ED contribution shows the asymmetric pattern of a Fano resonance.) [A. Miroshnichenko]
The case of a subwavelength nanodisk illuminated by a plane wave illustrates this light scattering (see figure at left). For dielectric nanodisks in particular, incident radiation brings both electric and magnetic responses of comparable strengths. The coupling of incoming light to the electric field’s circular displacement current results in a strong magnetic dipole resonance, owing to the field penetration and phase retardation inside the particle. The magnetic resonance occurs when the wavelength inside the particle becomes comparable to its spatial dimension—that is, when 2R ≈ λ/n, where n is the refractive index of nanoparticle material, R is the nanoparticle radius, and λ is the light’s wavelength.
This geometrically determined resonance suggests that the nanoparticle must have a relatively large refractive index to have resonances in visible and infrared (IR) spectral regions. Moreover, at the wavelength of magnetic resonance, the excited magnetic dipole mode of a dielectric nanoparticle may become comparable to, or even stronger than, the electric dipole response—and thereby provide a major contribution to the scattering efficiency. Finally, and importantly, the electric and magnetic dipoles are excited along the corresponding incident field components and perpendicular to each other.
For many years, physicists viewed the displacement current, introduced by James Clerk Maxwell in his famous equations, as a mathematical curiosity, devised mainly to provide continuity of the current lines in non-conducting media in which the induction, D, changes with time. Yet within the framework of resonant all-dielectric photonics driven by strong electric and magnetic dipole and higher-order multipole Mie resonances, as the brief analysis above suggests, the displacement current becomes a powerful tool, helping to realize optical magnetism in low-loss, highly efficient nanophotonic structures.
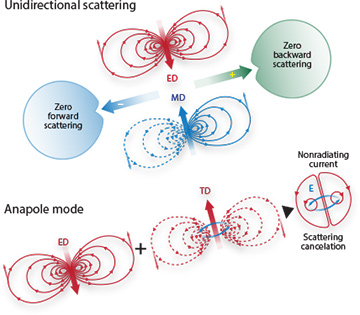
Emission patterns generated by pairs of dipoles of different origin. (Top) Constructive interference of magnetic and electric dipole moments can result in zero backward scattering (analogous to the Kerker condition); destructive interference can result in zero forward scattering. (Bottom) The cancellation of the radiation patterns of the electric and toroidal dipole moments, with the creation of a virtually nonradiating anapole mode. [Illustration by Phil Saunders]
Multipole and multimode interference
A key element in understanding light scattering on nanoscale objects—and applying it practically—is understanding the multipole decomposition of electromagnetic fields. This framework describes the scattering intensities and radiation pattern of dominant excited multipole modes.
For spherical metallic nanoparticles, the electric dipole mode usually dominates the Mie scattering with a symmetric radiation pattern. By contrast, for dielectric particles, the generation and interference of multipolar modes becomes important, and begins to enable nanoscale manipulation of light and exquisite control of the scattering direction (see figure at right).
Similar multipole modes: Fano resonances. In the simplest case, when all multipole modes are of the same type, the optical properties of all-dielectric nanoparticle structures resemble their plasmonic analogues. In particular, such nanoparticle structures often demonstrate sharp Fano resonances (resonances with characteristic asymmetric scattering profiles due to interference between sharp resonant and broad non-resonant modes). However, two major differences exist between plasmonic systems and systems involving high-index dielectric nanoparticles. First, dielectric particles exhibit much lower losses, which allows observation of Fano resonances in many geometries not available for plasmonics. And, second, magnetic dipole resonances of individual dielectric particles play a crucial role in the appearance of the Fano resonances.
Electric and magnetic dipole moments: unidirectional scattering. Incorporating the optical magnetic response provides an extra degree of freedom for efficient light control, through interfering electric and magnetic dipoles and multipoles. For example, interference between the electric and magnetic dipole modes can lead to simultaneous enhancement of forward scattering and suppression of backward scattering. In high-index dielectric nanoparticles, strong directional scattering of light can be realized due to interference of magnetic and electric dipole responses excited simultaneously with comparable strength.
Finding the right materials
The spectral position of the nanoparticle’s magnetic dipole resonance depends directly on its refractive index; thus, visible-wavelength operations require high-index materials. The field enhancement and quality factor of Mie resonances also benefit when the particle has a large index, as a larger index contrast means a smaller radiation leakage from the nanoparticles.
These considerations have spurred a quest for high-refractive-index materials. In the visible and NIR spectral ranges, semiconductors such as Si, Ge and AlGaAs all have large permittivity values. In the neighboring mid-IR range, also of great interest to nanophotonics, narrowband semiconductors such as Te and PbTe, and polar crystals such as SiC, have already been implemented for all-dielectric metadevices operating with Mie resonances.
An early milestone in this field was the experimental observation of the strong magnetic response of spherical Si nanoparticles in the visible and IR bands, reported almost simultaneously in 2012 by two research groups. This opened a new avenue toward studying many interesting phenomena using high-index dielectric structures as building blocks for metadevices—driven by inspiration from the century-old study of light scattering, but placed on a new platform of meta-optics.
 Optical magnetic response of Si nanospheres, shown for optical dark-field and SEM images. [A.I. Kuznetsov et al., Sci. Rep. 2, 492 (2012)]
Optical magnetic response of Si nanospheres, shown for optical dark-field and SEM images. [A.I. Kuznetsov et al., Sci. Rep. 2, 492 (2012)]
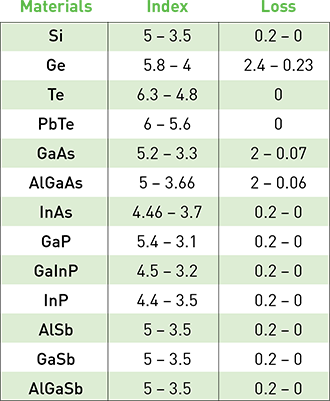 Materials in visible and IR: Refractive indices and absorption coefficients for high-index materials available in the visible and IR spectral regions.
Materials in visible and IR: Refractive indices and absorption coefficients for high-index materials available in the visible and IR spectral regions.
This is conceptually similar to the so-called Kerker condition—the condition for the zero backward scattering, ε = µ, derived by M. Kerker in 1983 for a hypothetical magnetic particle having similar electric and magnetic properties. It is also possible to derive an analogous condition for minimizing the ratio of forward to backward.
Electric and toroidal dipole moments: optical anapole mode. The interference of electric and magnetic dipole modes offers only one example of a larger class of multipolar interference effects observable with dielectric particles. Perhaps most interesting is the interference of the electric dipole and toroidal dipole moments, which can suppress far-field radiation to create a virtually nonradiating source called an optical anapole mode.
Though the toroidal multipoles play an essential role in expansions for arbitrary charge-current distributions, they have not attracted much attention until recently—largely because, in the far field, toroidal multipoles are identical to their electric multipolar counterparts. At the same time, conventional multipole expansions are usually confined to charge-current distributions that are far smaller than the effective wavelength, where the contributions of toroidal multipoles are negligible. Isolated excitation of toroidal multipoles requires careful engineering of the nanoparticle structure to match the special corresponding near-field current distributions; still, even simple homogeneous dielectric particles with Mie resonances can support toroidal dipole moments, co-exciting with the electric and magnetic multipoles.
Indeed, because the electric and toroidal dipoles have identical scattering patterns, they can cancel each other in the far field, and appear to be invisible, when co-excited and spatially overlapped with the same scattering magnitude, but out of phase. This is the basic mechanism for nonradiating optical anapoles, which were only recently discovered.
A pure nonradiating anapole excitation requires both the proper electric dipole and toroidal dipole excitation and the suppression of other multipoles—something impossible for homogeneous spheres or cylinders with incident plane waves, as the magnetic dipole mode and other quadrupole excitations at the scattering cancelling point are not negligible. Recently, however, optical anapoles have been experimentally demonstrated in both silicon and germanium nanodisks. One fundamental question at present is whether these special modes with suppressed far-field radiation can support stimulated light amplification in the form of a near-field anapole nanolaser.
Planar optics with transparent metasurfaces
An understanding of multipole decomposition, and of the different interference effects among electric, magnetic and toroidal multipole modes of high-index dielectric nanoparticles, offers a toolkit for many applications, including controlled radiation in nanoantennas, unconventional Brewster angle, directional harmonic generation, spontaneous parametric down-conversion, polarization tomography, and other areas. In this section, we look at one application in particular: using the interference of electric and magnetic dipole modes to create highly transparent metasurfaces with high-index dielectric nanoparticles.
Such metasurfaces constitute a rapidly growing area of research, as a logical extension of metamaterials toward their practical application in planar optics. Dielectric metasurfaces in particular offer the potential for engineering electric and magnetic optical responses within low-loss, thin-layer structures. Rooted in earlier studies of frequency-selective surfaces in radiophysics, the field has been enriched and re-energized in recent years the recent progress in meta-optics and nanophotonics.
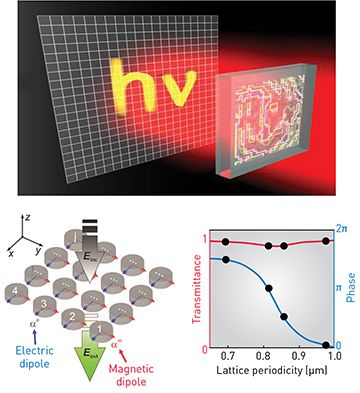 Huygens’ metasurfaces arise from the interference of electric and magnetic dipole modes satisfying the Kerker condition. This concept allows creation of different types of flat optical metadevices—such as wave plates, polarization converters, and holograms—with a very high transmission efficiency and an accumulated 2π phase change. [M. Decker et al., Adv. Opt. Mater. 3, 813 (2015)]
Huygens’ metasurfaces arise from the interference of electric and magnetic dipole modes satisfying the Kerker condition. This concept allows creation of different types of flat optical metadevices—such as wave plates, polarization converters, and holograms—with a very high transmission efficiency and an accumulated 2π phase change. [M. Decker et al., Adv. Opt. Mater. 3, 813 (2015)]
In the realm of high-index dielectric nanoparticles in particular, we can combine many nanoparticles as “meta-atoms” to create a lattice of optically resonant, dielectric scatterers into an optical metasurface—a thin-layer, subwavelength-patterned planar structure that interacts strongly with light in ways that depend on the characteristics of their composite elements. In particular, by employing different types of multipole interference effects, we can create resonant dielectric metasurfaces with a variety of useful functionalities that employ both electric and magnetic responses to control the phase of incoming light. One recent example lies in novel Huygens’ metasurfaces and metadevices that rely on the suppression of backward scattering due to the interference of electric and magnetic dipole modes (that is, due to the first Kerker condition).
Such dielectric metasurfaces, in marked contrast to plasmonic metasurfaces, offer very high efficiencies in transmission—exceeding, in some cases, the efficiency of a glass plate. They also can demonstrate higher efficiencies in the reflection regime, showing reflection better than that of a metallic plate. But dielectric surfaces have an additional advantage: they allow the imprinting of different types of phase patterns by using two types of dipole resonances (or, more generally, two types of multipoles). Specifically, each dipole resonance shifts the phase of the propagating wave from 0 to π near the resonance, so that two dipoles at the same wavelength and location may cover the whole 0-to-2π phase range.
Planar metadevices based on dielectric nanostructured surfaces with both electric and magnetic Mie-type resonances demonstrate the best efficiency to date for functional flat optics. They have had only one disadvantage: a narrow operational bandwidth. Very recently, however, S. Kruk and colleagues were able to demonstrate broadband transparent metasurfaces that allowed highly efficient manipulation of polarization. Inspired by the ideas of multilayer coating, they used a superposition of the scattering contributions from several electric and magnetic multipolar modes of the constituent meta-atoms to achieve destructive interference in reflection over a large spectral bandwidth. Employing that novel concept, they demonstrated almost reflectionless half-wave plates, quarter-wave plates and vector beam q-plates that operate across multiple telecom bands with roughly 99 percent polarization conversion efficiency.
 (Left) Mie resonances allow a two-order-of-magnitude enhancement of the third-harmonic signal in Si nanodisks. (Right) Control of the directionality of second-harmonic generation radiation patterns from AlGaAs nanodisks on a glass substrate. [M.R. Shcherbakov et al., Nano Lett. 14, 6488 (2014) / R. Camacho-Morales et al., Nano Lett. 16, 7191 (2016)]
(Left) Mie resonances allow a two-order-of-magnitude enhancement of the third-harmonic signal in Si nanodisks. (Right) Control of the directionality of second-harmonic generation radiation patterns from AlGaAs nanodisks on a glass substrate. [M.R. Shcherbakov et al., Nano Lett. 14, 6488 (2014) / R. Camacho-Morales et al., Nano Lett. 16, 7191 (2016)]
A new era of nonlinear nanophotonics
Even more exciting applications of meta-optics based on Mie resonances lie in nonlinear nanophotonics—a rapidly developing research field with potential applications in nonlinear nanoantennas, light sources and ultrafast miniature devices. Extensive theoretical and experimental studies of nonlinear optical properties in metallic nanoparticles have already laid the foundation of contemporary nonlinear plasmonics. In many cases, however, all-dielectric systems can offer stronger nonlinear effects—as well as novel functionalities enabled by pronounced magnetic dipole and higher-order Mie-type resonances.
Tight confinement of the local electromagnetic fields in resonant photonic nanostructures can boost nonlinear optical effects, thus providing versatile opportunities for the subwavelength control of light. Recent progress of all-dielectric nanophotonics, where the electric and magnetic multipolar contributions can become comparable, have led to advances in the emerging field of multipolar nonlinear nanophotonics. This field involves the enhancement of nonlinear effects in all-dielectric nanostructures due to multipolar Mie-type resonances and optically induced magnetic response—and it could ultimately lead to novel nonlinear photonic metadevices operating beyond the diffraction limit.
In one recent example, Maxim Shcherbakov and colleagues demonstrated a strong enhancement of third-harmonic generation (THG) using both isolated and arrayed silicon nanodisks that were optically pumped in the vicinity of the magnetic dipole resonance. Because the magnetic dipole resonance features significantly enhanced local fields, tightly bound within the volume of the nanoscale resonators, and because the third-order polarization scales with the local electric field cubed, the silicon nanodisks, pumped by resonant laser radiation, considerably boosted the resonant THG response—by a factor of up to 100 compared with the THG from bulk silicon. The generated 420-nm radiation was bright enough to be observed by the naked eye under the table-lamp illumination.
Combining nanodisks into clusters provides another degree of freedom in tailoring the nonlinear response. In particular, strong reshaping of the third-harmonic spectra was observed for quadrumers of silicon nanodisks near the condition of the magnetic Fano resonance and for Ge particles satisfying the condition for the excitation of the anapole mode. Complex patterns in measured THG spectra have also been substantiated by interference of nonlinearly generated waves radiated by different parts of the sample and augmented by an interplay between electric, magnetic, and toroidal dipole moments in the nanodisks.
Even more important is designing radiation patterns and polarization for nanoantennas that can interact strongly with the incoming light and can transform its frequency, radiation and polarization patterns. Very recently, Rocio Camacho-Morales and colleagues demonstrated dielectric AlGaAs nanoantennas for efficient second-harmonic generation (SHG), enabling control of both directionality and polarization of nonlinear emission. The key lay in specialized III-V semiconductor nanofabrication of high-quality AlGaAs nanostructures embedded in optically transparent, low-index material, thereby allowing for simultaneous forward and backward nonlinear emission. The group showed that nanodisk AlGaAs antennas can emit the second harmonic in a preferred direction, with a backward-to-forward ratio up to five, and can also generate complex vector polarization beams, including beams with radial polarization.
These constitute just a few examples of how strong electric and magnetic resonances and their interference in high-index dielectric nanostructures are bringing new physics to simple geometries—and, as a result, opening unique prospects for constructing optical nanoantennas with reduced dissipative losses and considerable enhancement of the nonlinearly generated fields. We believe that these developments will drive rapid progress in engineering nonlinear optical effects beyond the diffraction limit, with important implications for novel nonlinear photonic metadevices operating at the nanoscale.
All-dielectric nanophotonics could employ all of the advantages of optical magnetic resonances to create a new generation of nanoantennas, nanolasers, metasurfaces and metadevices.
Outlook
The meta-optics of dielectric nanoparticles and subwavelength structures, based on the physics of the Mie resonances, is beginning to equip the modern study of metadevices with a new variety of optically induced electric and magnetic dipole and multipole resonances. As a result, high-index nanophotonic structures could soon start to complement, or even supplant, plasmonic components in a range of metadevice applications. All-dielectric resonant structures bring many advantages to the table: resonant behaviour, low energy dissipation into heat and stronger nonlinear effects.
Perhaps above all, the ability to simultaneously excite strong electric and magnetic dipole and multipole modes—and, in turn, to exploit constructive or destructive interferences—allows for unusual beam-shaping and the resonant enhancement of magnetic fields in dielectric nanoparticles. That, in turn, is likely to spawn a variety of novel applications in both linear and nonlinear optics. Indeed, we expect that all-dielectric nanophotonics will ultimately employ all of the advantages of optical magnetic resonances—including Raman scattering, magneto-optical effects, nonlinear parametric interactions and integrated quantum photonics—to create a new generation of nanoantennas, nanolasers, highly efficient metasurfaces and ultrafast metadevices.
The authors are indebted to the Australian Research Council for support, and also thank many of their numerous colleagues and collaborators for helping to develop this new, exciting field.
Yuri Kivshar and Andrey Miroshnichenko are with the Nonlinear Physics Center of the Research School of Physics and Engineering, the Australian National University, Canberra, Australia.
References and Resources
-
N. Zheludev and Y.S. Kivshar. “From metamaterials to metadevices,” Nat. Mater. 11, 917 (2012).
-
A.B. Evlyukhin et al. “Demonstration of magnetic dipole resonances of dielectric nanospheres in the visible region,” Nano Lett. 12, 3749 (2012).
-
A.I. Kuznetsov et al. “Magnetic light,” Sci. Rep. 2, 492 (2012).
-
A.E. Miroshnichenko and Y.S. Kivshar. “Fano resonances in all-dielectric oligomers,” Nano Lett. 12, 6459 (2012).
-
I. Staude et al. “Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks,” ACS Nano 7, 7824 (2013).
-
M.R. Shcherbakov et al. “Enhanced third-harmonic generation in silicon nanoparticles driven by magnetic response,” Nano Lett. 14, 6488 (2014).
-
A.E. Miroshnichenko et al. “Nonradiating anapole modes in dielectric nanoparticles,” Nat. Commun. 6, 8069 (2015).
-
M. Decker et al. “High-efficiency dielectric Huygens’ surfaces,” Adv. Opt. Mater. 3, 813 (2015).
-
S. Kruk et al. “Broadband highly efficient dielectric metadevices for polarization control,” APL Photonics 1, 030801 (2016).
-
D.A. Smirnova and Y.S. Kivshar. “Multipolar nonlinear nanophotonics,” Optica 3, 1241 (2016).
-
R. Camacho-Morales et al. “Nonlinear generation of vector beams from AlGaAs nanoantennas,” Nano Lett. 16, 7191 (2016).
-
A.I. Kuznetsov et al. “Optically resonant dielectric nanostructures,” Science 354, 6314 (2016).
