 LuckyCam mounted on the ESO New Technology Telescope (La Silla, Chile).
LuckyCam mounted on the ESO New Technology Telescope (La Silla, Chile).
The Hubble Space Telescope (HST) has revolutionized astronomy. Its cameras have delivered a resolution that is 10 times higher than what is achievable on the ground, allowing astronomers to capture photos with unimaginable detail.
But Hubble’s lifetime is limited. Earlier this year, it was refurbished for the last time, and no plans are under way to develop other space-based telescopes that will yield visible images with the same level of detail. When HST inevitably fails, astronomers will expect instrument designers to deliver high-resolution images from ground-based telescopes.
Unfortunately, however, turbulence in the upper atmosphere has made that difficult. Such turbulence produces micro-thermal fluctuations that cause phase errors to degrade the incoming beam from distant astronomical objects.
To address this, astronomers typically use adaptive optics (AO) to detect phase errors across the wavefront entering a telescope and use a deformable optical system to compensate for those errors in real-time, yielding an image that is much closer to being diffraction-limited. Nearly $1 billion has been spent to date on AO programs in astronomy, but the results have been mixed at best.
In the near-infrared (1.6-2.2 µm), AO systems have delivered HST resolution images on 8- to 10-m-class telescopes. But in the visible part of the spectrum—which is very important in astronomy—adaptive optics has been much less successful. (Despite the recent emphasis on infrared telescopes, the fact is that we know much more about the physics of stars, nebulae and galaxies in the visible part of the spectrum than any other.)
There is hope, however. Recent results suggest that a radically different approach might be more productive, particularly in the visible part of the spectrum. In fact, Hubble resolution has already been demonstrated in the visible on Hubble-size ground-based telescopes. More than 30 years ago, David L. Fried suggested a technique that he coined as “Lucky Imaging,” which utilizes the stochastic nature of turbulence. If we take images fast enough to freeze the motion caused by atmospheric turbulence, there will be instances when the phase fluctuations are significantly smaller than average. The best images may then be selected and combined to give much higher resolution than would otherwise be possible.
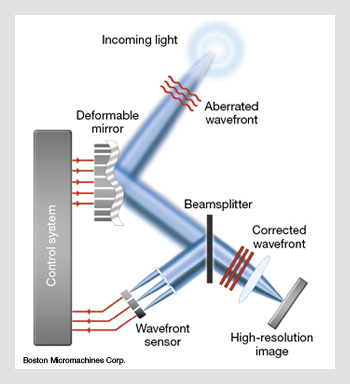 General setup of an adaptive optics system. The wavefront sensor (here shown as a Shack-Hartmann sensor) determines the phase errors in the input wavefront. These errors are processed and generate signals to drive a deformable mirror, which corrects the wavefront and provides a higher-resolution image on the detector.
General setup of an adaptive optics system. The wavefront sensor (here shown as a Shack-Hartmann sensor) determines the phase errors in the input wavefront. These errors are processed and generate signals to drive a deformable mirror, which corrects the wavefront and provides a higher-resolution image on the detector.
Where we are with adaptive optics
Most AO instruments use Shack-Hartmann sensors that subdivide the wavefront with a lenslet array to provide an array of images of a reference star. The positional errors in these star images are used to compute the wavefront distortions, which are then corrected with a fast deformable mirror. Large telescopes require a great number of lenslets, and the positions need to be updated on a timescale shorter than the decorrelation time, t0, which is approximately the time it takes for the wind to blow across a typical turbulent cell diameter of r0. The r0 diameter is known as the Fried parameter; it characterizes the median cell diameter over which the phase variance is 1 radian.
These constraints force a requirement for a reference star that must be several hundred times fainter than the faintest naked-eye star yet still bright enough that the chance of finding one in close proximity to a scientifically interesting target is negligibly small. Nevertheless, some very pretty images have been achieved with these techniques. Since stars are generally brighter in the near infrared, and r0 is bigger in the infrared (so fewer lenslets and a slower correction speed can be used), adaptive optics has been applied most successfully at those wavelengths.
Lasers are also being used to generate artificial reference stars in the sky. In principle, they can allow astronomers to generate a reference object anywhere they desire. However, the improvement in resolution that they allow is limited, since the artificial laser stars themselves are generated by passing through the turbulent atmosphere and thus are not very sharp.
Disappointingly, astronomers have not yet demonstrated an AO system on a Hubble-sized telescope that works in the visible and can deliver the HST’s resolution of about 0.1 arcsecond. It is therefore difficult to believe that even higher resolutions could be realized on the planned next-generation telescopes, which have diameters 5-20 times that of Hubble’s and have a theoretical resolution of only a few milliarcseconds.
Getting Lucky
A group at the Institute of Astronomy of the University of Cambridge in England is pursuing the Lucky approach. We have built high-speed cameras that use the latest electron-multiplying CCD chips, which allow true photon counting performance even at high frame rates. Other groups have since produced similar instruments. By selecting 10-30 percent of images, they find that, on a Hubble-sized (2.5-m diameter) telescope on a good observing site such as on the Nordic Optical Telescope on La Palma in the Canary Islands, they routinely produce images that are very similar in resolution to that of Hubble in the visible.
Lucky works by selecting those moments when the instantaneous average turbulent cell size across the aperture, r0, is largest. Unlike AO techniques—which give a very small isoplanatic patch size (the area of sky over which images are reasonably well corrected, generally a few arcseconds in the visible for standard AO systems)—Lucky typically produces isoplanatic patch sizes of nearly 1 arcminute in diameter.
 Globular cluster before and after Lucky Cam. (Top) Image of the center of the globular cluster on the Caltech Palomar 5-m telescope under good observing conditions (~0.6 arcsec seeing). (Bottom) More detailed image taken with the Lucky Camera attached to the PALMAO low-order adaptive optic system. Both images cover a tiny area, only 10 x 10 arcseconds, smaller than the width of a human hair held at full stretch of your arm. This is the highest resolution image ever taken in the visible or infrared.
Globular cluster before and after Lucky Cam. (Top) Image of the center of the globular cluster on the Caltech Palomar 5-m telescope under good observing conditions (~0.6 arcsec seeing). (Bottom) More detailed image taken with the Lucky Camera attached to the PALMAO low-order adaptive optic system. Both images cover a tiny area, only 10 x 10 arcseconds, smaller than the width of a human hair held at full stretch of your arm. This is the highest resolution image ever taken in the visible or infrared.
Unfortunately, these techniques cannot be used directly for larger telescopes, since the probability of getting a good sharp image rapidly becomes vanishingly small. For example, conditions that produce 20-percent acceptable images on a 2.5-m telescope would only yield a few images in a billion on the 10-m telescope! Clearly, a different approach is needed.
The ideal system would incorporate the use of very faint reference stars so that the technique could be used over the entire sky. The approach should also deliver a good isoplanatic patch size. This is critical, since astronomy relies on the observation of new objects so that they can be catalogued and compared with known ones. If the resolution of an image changes over very short angular scales, it becomes almost impossible to know whether adjacent objects are genuinely of a different size or appearance or whether the corrections introduced by the image correction system are responsible for the variations. The technique should be fairly efficient and easy to set up, since large telescope time is at a premium, and the high-resolution images generated should be capable of being delivered to the multi-object spectrographs that are currently in use.
There are many more faint stars in the sky than there are bright ones, so if we need to find one within one arcminute of a random position in the sky, we can infer that we need to work with reference stars several hundred times fainter than those required for Shack-Hartmann sensors. Although such stars are faint, they will yield as many as 10,000 detected photons per second on a large (8-10 m class) telescope. What can be done with such photon rates?
The distribution on the size of wavefront distortions due to turbulence approximately follows Kolmogorov’s Law. This means that most of the turbulent power is on the largest scales, with progressively less power on smaller and smaller scales. The largest scales correspond to tip-tilt, then defocus, astigmatism, coma, etc. The turbulent cell size, r0, will be increased substantially if the variance across it due to these largest scales could be removed. If this is done and the effective value of r0 is adequately increased, then we can use Lucky imaging techniques. However, conventional AO strategies involving fast-readout Shack-Hartmann techniques simply cannot work on stars as faint as the ones we need to detect.
Curvature sensing
Curvature sensors are an alternative approach to wavefront sensing. Rene Racine has shown that curvature sensors are typically tenfold more sensitive that Shack-Hartmann sensors when used for relatively low-order AO correction. Here, light from a distant star illuminates a pupil plane. Images are formed on either side of this pupil plane, which corresponds to the entrance aperture of the telescope. As the beam passes through the pupil, it becomes less intense if the wavefront is diverging and more intense if it is converging.
Imaging detectors allow this to be measured directly, and the phase errors across the wavefront can be deduced so that a deformable mirror may be used to correct the errors. In practice, one can obtain better results by using four separate planes, two on either side of the real pupil plane, since the propagation of the wavefront is nonlinear. If we are only interested in errors on the largest scales, their detection becomes much easier.
This is because the large-scale errors change relatively slowly. For example, the defocus error will change only when the essentially frozen phase screen is blown across a significant part of the telescope aperture by the wind. At the Paranal site of ESO’s Very Large Telescope in Chile, typical wind speeds are about 6-7 m/s; thus, it takes more than a second to cross the diameter of an 8-m telescope. It is therefore possible to accumulate phase-error information on the largest scales using much longer exposure times (fractions of a second) than could be used with a Shack-Hartmann sensor, which may be read out many hundreds of times per second.
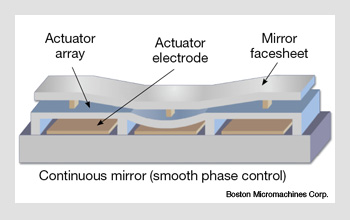 MEMS deformable mirror cross-section. Applying an array of electrical potentials to the electrodes causes the mirror to be deformed. By reflecting the input wavefront with such a device, one can compensate for the phase errors in the incoming wavefront. MEMS deformable mirrors are available with more than 1,000 elements in total.
MEMS deformable mirror cross-section. Applying an array of electrical potentials to the electrodes causes the mirror to be deformed. By reflecting the input wavefront with such a device, one can compensate for the phase errors in the incoming wavefront. MEMS deformable mirrors are available with more than 1,000 elements in total.
The light from the reference star is directed toward the curvature sensor, which projects the four pupil images side-by-side onto a detector. By using the same high-efficiency photon counting detectors that are used for the Lucky imaging experiments, we can measure and remove much of the turbulent power on these large scales. The curvature signal is used to drive a deformable mirror that uses MEMS technology, such as those made by Boston Micromachines.
By removing the power corresponding to the first 10 Zernike terms (those corresponding to tip-tilt, focus, astigmatism and coma), astronomers can reduce the turbulent power by a factor of 25. That is equivalent to increasing the size of r0 by a factor of five, so we would expect to have the same probability of getting a Lucky image on a 2.5-m telescope as we would on a telescope five times the diameter of Hubble when used with this low-order AO correction system.
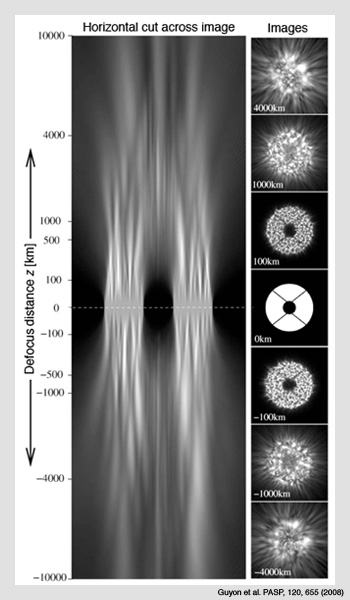 An image of the pupil as a function of defocus distance. The image was created using simulations from Olivier Guyon of the Subaru telescope project in Hawaii. The very-small-scale turbulent structure is most easily seen close to the pupil, while further away from the pupil plane the images are dominated by the largest scales of turbulence. By combining the images, it is possible to compute the phase errors in the wavefront. Careful selection of the position of the image planes is critical for high efficiency. Ideally, four images are arranged side-by-side on a high-speed electron multiplying CCD camera running in photon-counting mode.
An image of the pupil as a function of defocus distance. The image was created using simulations from Olivier Guyon of the Subaru telescope project in Hawaii. The very-small-scale turbulent structure is most easily seen close to the pupil, while further away from the pupil plane the images are dominated by the largest scales of turbulence. By combining the images, it is possible to compute the phase errors in the wavefront. Careful selection of the position of the image planes is critical for high efficiency. Ideally, four images are arranged side-by-side on a high-speed electron multiplying CCD camera running in photon-counting mode.
Olivier Guyon of the Subaru telescope project in Hawaii has investigated these techniques. He suggests that such an approach will be very effective and that it will indeed be possible to use very faint reference stars effectively. Indeed, we could also use the light from compact galaxies as reference objects—provided that they are small enough to have a constant phase across the image.
Lucky goes large
In order to confirm that Lucky Imaging can be used on much larger telescopes (provided that much of the power on the largest turbulent scales is removed), we mounted our Lucky camera behind PALMAO, the relatively low-order adaptive optics system on the Palomar 5-m telescope operated by Caltech in Calif., U.S.A. The results were very encouraging indeed.
The images that were taken with this degree of correction combined with Lucky Imaging are in fact the highest-resolution images ever obtained in the visible on any telescope, with a resolution about three times that of Hubble. (The cameras on Hubble under-sample the images so that HST’s resolution is significantly poorer than its theoretical diffraction limit.) The images have a resolution of about 35 milliarcseconds (mas), close to the diffraction limit of the Palomar 5-m telescope at 750 nm, where those observations were made.
We also found that a relatively high fraction of images were sharp, typically 30 percent, further improving the efficiency of the method. Our results suggest that the technique should work well with even the largest current telescopes on Earth. For example, with the VLT 8-m telescopes, we would expect to reach close to 20 mas resolution and about 16 mas resolution on the Keck 10-m telescopes.
In addition, we have been trying to understand what limits the isoplanatic patch size to around one arcminute in diameter. The patch size is defined as the radius at which the the brightness of the core of the image is reduced by a factor of 1/e. We see that the core of the image progressively becomes attenuated as we measure objects further from the reference star. The cores of stars further from the reference star become elongated in a direction toward the reference star, and that is what is responsible for the reduction in apparent sharpness.
The elongation is, in turn, caused by the fact that the tip-tilt errors are not constant across a wide field but are slightly different for various areas of the image. As we saw before, the tip-tilt error changes relatively slowly, so we have the opportunity (at least in principle) to look at individual frames and measure the positions of objects in those frames.
We then construct a rubber sheet distortion pattern for each image, so that each may be transformed onto a proper rectangular grid before it is combined into the summed images. We can use even fainter objects in the field to calibrate these distortions, since they are small and slowly varying and in this way substantially increase the isoplanatic patch size.
 Electron-multiplying CCDs are at the heart of Lucky Cam technologies. Noiseless internal amplification allows for the readout noise to be effectively reduced. The Lucky Imaging camera typically runs with a gain of about 2,000, giving a signal-to-noise on an individual photon of about 20:1. Recent developments of this technology—funded by the European Southern Observatory—have produced a device of 240 x 240 pixels. With eight electron-multiplying outputs working in parallel, the device can operate at up to 1,500 frames per second in photon counting mode.
Electron-multiplying CCDs are at the heart of Lucky Cam technologies. Noiseless internal amplification allows for the readout noise to be effectively reduced. The Lucky Imaging camera typically runs with a gain of about 2,000, giving a signal-to-noise on an individual photon of about 20:1. Recent developments of this technology—funded by the European Southern Observatory—have produced a device of 240 x 240 pixels. With eight electron-multiplying outputs working in parallel, the device can operate at up to 1,500 frames per second in photon counting mode.
Our simulations suggest that we should expect an isoplanatic patch size as large as 3-5 arcminutes in diameter. We have made very recent observations using an array of four electron-multiplying CCDs configured optically to give a contiguous image size of about 4,000 x 1,000 pixels. Early results suggest our model predictions are correct.
The same techniques may be used just as easily in the near-infrared. At longer wavelengths, both r,0 and t0 are larger so that these methods become progressively easier to implement. The readout rates required in the infrared must be reasonably fast (the wind speed does not change), but photon counting is much less important since photon flux rates are generally much higher in the infrared.
The application of these methods as a way of feeding high-resolution visible spectrographs should be relatively straightforward. Many modern spectrographs now use integral field units. These consist of an array of micro-lenses in the telescope image plane. The light striking each micro-lens is fed into a fiber and the bundle of fibers taken to the spectrograph. The output of the many fibers are placed in a line to look like the slit of a conventional spectrograph. Combining these with a similar fiber bundle at a nearby reference star, close enough so that the phase distortions are also well corrected, provides the guidance as to the alignment of the target object on the integral field unit array of lenses. It also indicates which moments provide the highest resolution.
Many of these techniques have now been demonstrated successfully. By accepting the loss inevitable when a significant fraction of the images are rejected, scientists can achieve much higher resolutions than are possible by any other means. All the techniques required to build high-resolution systems are now in place. The recent success of Lucky Imaging has been largely due to the introduction of new technologies, particularly electron multiplying CCDs, which allow fast-frame-rate cameras to detect photons with excellent signal-to-noise. Astronomers hope that they will be available for general use before too long. Undoubtedly, Lucky Imaging will allow astronomers to study yet fainter and more compact objects both near and far. It offers the exciting promise of a further leap in our understanding of the universe.
Craig Mackay is with the Institute of Astronomy, University of Cambridge, United Kingdom.
References and Resources
>> D.L. Fried. “Probability of getting a lucky short-exposure image through turbulence,” J. Opt. Soc. Am. A 68, 1651 (1978).
>> O. Guyon et al. “Improving the Sensitivity of Astronomical Curvature Wavefront Sensor Using Dual Stroke Curvature,” Publ. Astron. Soc. Pac. 120, 655 (2008).
>> R. Racine. “The Strehl Efficiency of Adaptive Optics Systems,” Publ. Astron. Soc. Pac. 118, 1066 (2006).
>> Lucky Imaging Web site
>> More information about MEMS deformable mirrors
>> Electron-multiplying CCDs are manu-factured by E2V technologies Ltd.
