Feature
Optical Tunable Dispersion Compensators Based onThermally Tuned Fiber Bragg Gratings
Fiber Bragg gratings are well positioned to respond to the growing need for more stringent control of dispersion compensation. Thermal tuning has proven to be an effective technique for achieving this goal.
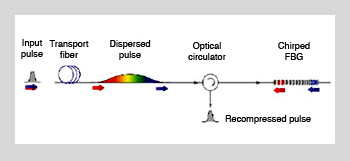
Pulse broadening due to chromatic dispersion Broadening occurs in transport fiber and recompression using a chirped fiber Bragg grating.
Tunable chromatic dispersion compensators are known to be critical components of 40 Gb/s systems. They are already required at 10 Gb/s, and there was an extensive deployment over the past 10 years of fixed dispersion compensation modules, mainly based on dispersion compensating fiber and, more recently, fiber Bragg gratings.
…Log in or become a member to view the full text of this article.
This article may be available for purchase via the search at Optica Publishing Group.
Optica Members get the full text of Optics & Photonics News, plus a variety of other member benefits.
