Feature
Optical Atomic Clocks—from Dream to Reality
Recent developments in atomic physics and laser technology, especially techniques for laser cooling and the manipulation of atoms, have enabled the realization of so-called Cesium fountain atomic clocks with relative accuracy approaching 4 x 10-16.
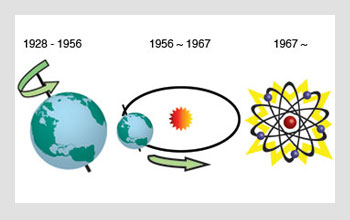
The changing definition of the “second”: (Left) 1s = 1/86,400 of a solar day; (center) 1s = 1/31,556,925.9747 of the tropical year; (right) 1s = 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atoms.
Time and timekeeping are among the most important aspects of human society. It is hard to imagine what life would be like without the presence of clocks, watches and cell phones to tell us what time it is.
…Log in or become a member to view the full text of this article.
This article may be available for purchase via the search at Optica Publishing Group.
Optica Members get the full text of Optics & Photonics News, plus a variety of other member benefits.
